Дәрістер. Бренстедтің негізгі теңдеуінің негізгі салдары.
Бренстед теңдеуінің бірінші салдары. Егер қышқылдық-негіздік әрекеттесуге бейтарап типтес қышқылдар (HCl, HNO3 және т.б.) қатысса, онда ZHA = 0, ал rA-≈ rS = r; ZHS+1-ге тең болсын. Сонда:
онда Демек, еріткіштің диэлектрлік өткізгіштігі жоғарылағанда тепе-теңдік константасы көбейеді, оған қоса молекулярлық қышқыл диссоциациясы да көбейеді. Егер рК = const + Бұдан зарядталмаған қышқылдар үшін тепе-теңдік константа көрсеткіші сусыз еріткіштің
6 кесте. Хлорлы органикалық қышқылдардың диэлектрлік өткізгіштігінен тепе-теңдік константа мәнінің тәуелділігі
8 CCl3COOH 6 CH3COOH 2 CH2ClCOOH HCOOH 0,1 0,2 0,3 0,4 1/D
1-сурет. Хлорлы қышқыл рК-ң сусыз еріткіштер (карбон қышқылдары) диэлектрлік өткізгіштігінің кері шамасына тәуелділігі. Бренстед теңдеуінің екінші салдары. Бренстедтің негізгі теориясына сүйене отырып қышқылдық күшінің кез-келген екі еріткіш табиғатына тәуелділігін табуға болады. Бейтарап қышқыл үшін ZHA = 1 и ZHS+= 1, rA-= rS = r
Берілген қышқыл үшін бірінші еріткіштегі протолиттік тепе-теңдік константасы:
Екінші еріткіште:
Әр түрлі екі еріткіштердегі протолиттік тепе-теңдік константасының айырмашылықтарын аламыз:
pKHAS2= const + pKHAS1 (14)
Бұл түзудің еңкею бұрышының тангенсі 1: tgα = 1-ге тең. Сонымен, екі түрлі еріткіштегі зарядталмаған (бейтарап) қышқылдардың протолиттік тепе-теңдік константалары көрсеткішінің айырмашылығы тұрақты шама болып табылады. Оны карбон қышқылының суда және бутанолда, суда және метанолдағы мысалдарынан көреміз.
7-кесте Карбон қышқылдарының рК мәндері а) суда және бутанолда б) суда және метанолда
Бренстед теңдеуінің үшінші салдары. Бренстед теңдеуі еріткіш табиғатына байланысты екі қышқылдың салыстырмалы күштерінің өзгерістерін көруге мүмкіндік береді. Бірдей зарядты қышқылдар ZHA1= ZHA2= ZHA* алайық. Берілген еріткіштегі бірінші қышқыл үшін Бренстед теңдеуін жазамыз:
Сол еріткіштегі екінші қышқыл үшін:
(15) теңдеуден (16) теңдеуді аламыз:
(17) теңдеуді жалпылай көрсетеміз:
(18) теңдеуден қорытатынымыз: бірдей зарядты екі қышқылдың түрлі еріткіштегі протолиттік тепе-теңдік константасының қатынасы 1/D-дан сызықты тәуелді. Мұны екі органикалық қышқылдың – хлорсірке және дихлорсірке қышқылдардың мысалдарында көрсетеміз. 8-кесте Сірке және бензой қышқылдарының ΔрК еріткіштердің диэлектрлік өткізгіштігіне тәуелділігі
*Бір еріткіштен екінші еріткішке ауысқанда белсенділік коэффициенттері қатты өзгеруі мүмкін. Сондықтан түрлі еріткіштердегі заттардың қасиеттерін салыстыруға болады, егер кішкене болса да ұқсастық болса, мысалы, бірдей зарядталған. Дегенмен, Бренстед және Лоуридің протолиттік теориясының барлық артықшылықтарына қарамастан, кемшіліктер де бар: 1. Бренстед көмірсутектерді протолиттік әрекеттесуге қатыспайтын заттарға жатқызады, сәйкесінше оны қышқылдар немесе негіздер деп санауға болмайды. Бірақ көмірсутектерде сутек бар және олар қышқылдық-негіздік қасиеттерге ие. 2. Протолиттік теория протондармен әрекеттеспейтін қосылыстардың қышқылдық-негіздік қасиеттерін түсіндірмейді. (Мысалы, күкірт диоксиді, SnCl4, AlCl3 және т.б.). Бұл заттар қышқыл ретінде жақсы танымал, бұлардың қасиеттері протондық емес еріткіштерде айқын байқалады. 3. Бренстед негізгі теңдеуді шығарғанда еріген бөлшектердің сольваттануын, еріткіштің өзіне тән спецификалық химиялық табиғатын ескермеген. Ол аниондар әрқашан сфералық пішінде болады деп болжаған және т.с.с. Осыған байланысты қышқылдар мен негіздердің теориясы бірқатар авторлармен (Льюис Г., Усанович М.И. және т.б.) жетілдірілді және дамытыла берді. Дегенмен, Бренстед пен Лоуридің теориясы аналитикалық химияда түрлі еріткіштердегі жиі кездесетін тепе-теңдіктерді бейнелеу үшін өте қолайлы.
|

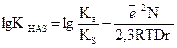 (10),
(10),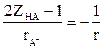 және
және 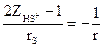 болғандықтан
болғандықтан
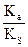 және
және 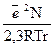 берілген қышқыл және еріткіш үшін тұрақты шама десек, (10) теңдеуді қарапайым түрде жазуға болады:
берілген қышқыл және еріткіш үшін тұрақты шама десек, (10) теңдеуді қарапайым түрде жазуға болады: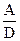 (11)
(11)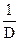 -дан сызықты функция екені шығады. Хлорлылау қышқылдар үшін бұл тәуелділік 6 кестеде және 1-суретте көрсетілген.
-дан сызықты функция екені шығады. Хлорлылау қышқылдар үшін бұл тәуелділік 6 кестеде және 1-суретте көрсетілген.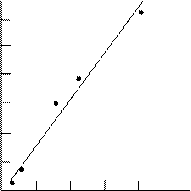 pKHClO4 CH3(CH2)2COOH
pKHClO4 CH3(CH2)2COOH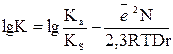
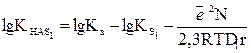 (12)
(12)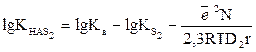 (13)
(13)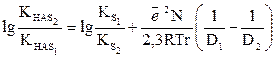
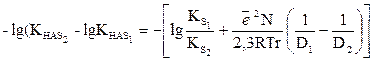 , онда
, онда




























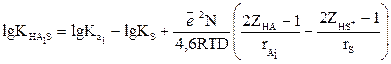 (15)
(15) (16)
(16)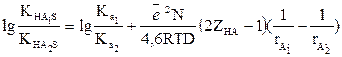 (17)
(17) (18)
(18)


