Назначение, структура и основные виды умозаключений

Высказывая некоторое суждение, мы считаем его либо истинным, либо более или менее правдоподобным. В первом случае будем говорить, что данное суждение признается со всей определенностью, а во втором – с некоторой степенью определенности. «Суждение признается со всей определенностью» означает то же, что и «имеется доказательство истинности этого суждения». «Суждение признается с некоторой степенью определенности» означает то же, что и «Имеются некоторые доводы в пользу истинности этого суждения, но отсутствует его доказательство». Естественно, что признание кем-либо некоторого суждения с некоторой степенью определенности отнюдь не означает, что это суждение объективно является истинным.

Основания, по которым признается некоторое суждение, могут быть разными. В одних случаях таким основанием является наблюдение, непосредственное восприятие какого-либо положения вещей или некоторой ситуации. Например, к признанию со всей определенностью суждения На моих часах половина первого склоняет наблюдение, т.е. непосредственное восприятие мною положения стрелок на циферблате часов. А когда я ищу ответ на вопрос, делится ли число 1569 на 3, утвердительный ответ я могу получить на основе суждения Если сумма цифр некоторого числа делится на 3, то и само это число делится на 3, истинность которого мне заранее известна, и суждения Сумма цифр этого числа делится на 3. Другими словами, искомый ответ я нахожу посредством следующего умозаключения:

1. Если сумма цифр некоторого числа делится на 3,

то и само число делится на 3.

2. Сумма цифр числа 1569 делится на 3

3. Число 1569 делится на 3.

Вы уже знаете, что суждения 1. и 2., признание которых склоняет к признанию суждения 3., в логике называют посылками,а суждение 3., признаваемое на основе суждений 1. и 2., именуют заключением. Мыслительный процесс, в котором на основе признания посылок осуществляется переход к признанию заключения, называют умозаключением. Черта, отделяющая заключение от посылок, прочитывается в этой записи как «следовательно» («значит», «в силу этого»).

Умозаключение не является суждением (хотя и формируется из суждений), и потому не может характеризоваться как истинное либо ложное: таковыми могут быть только посылки или заключение. Не любой переход от признания одних суждений к признанию другого является логически безупречным (правильным, или корректным): необходимо, чтобы заключение выводилось из посылок по правилам логики. Так, не является правильным умозаключением последовательность истинных суждений:

Все судьи имеют высшее юридическое образование.

Иванов П.К. – женатый мужчина.

Иванов П.К. увлекается классической музыкой.

Черта, отделяющая посылки от заключения и символизирующая обоснованность заключения этими посылками, здесь вообще не уместна. А вот ранее приведенная последовательность суждений является правильным умозаключением, равно как и нижеследующая:

Все адвокаты имеют высшее юридическое образование.

Иванов П.К. – адвокат.

Иванов П.К. имеет высшее юридическое образование.

В любом корректном умозаключении признание посылок побуждает нас к признанию заключения, что обусловлено истинностью его посылок и его логической правильностью. Различают логические правила двух видов: дедуктивные, гарантирующее истинность заключения при истинности посылок, и индуктивные, обеспечивающее при этих же условиях лишь повышение степени правдоподобия заключения (вероятности его истинности). Соответственно, умозаключения, в которых из посылок заключение выводится по дедуктивным правилам, называются дедуктивными, а если по индуктивным правилам – именуются индуктивными.

1. Правильность дедуктивных умозаключений не зависит от конкретного содержания входящих в них суждений. Она зависит только от логической формы этих суждений, т.е. способа связи терминов по объему в простых суждениях и смыслом логических союзов в сложных суждениях. Покажем это на примере:

(I) 1. Преступление – наказуемо.

2. Дача взятки – преступление.

3. Дача взятки – наказуема.

Отвлечемся от содержания дескриптивных терминов, входящих в состав посылок и заключения, заменив слово «преступление» параметром М, слово «наказуемо» (т.е. выражение «наказуемое деяние») – параметром Р, выражение «дача взятки» – параметром S. Введем количественные характеристики суждений, составляющих посылки и заключение, а также слово «суть», указывающее на включение одного множества предметов в другое, более широкое. Получаем:

(II) 1. Все М суть Р

2. Все S суть М

3. Все S суть Р

Данная структура называется формальной схемой умозаключения (I), поскольку входящие в него знаковые структуры 1.-3. являются уже не суждениями, а логическими формами (или формулами) этих суждений. Если теперь в этой схеме подставить на места М, Р и S другие (попарно различные) дескриптивные термины, мы вновь получим умозаключение, в котором при истинности посылок заключение с «железной» необходимостью также будет истинным. Приведем еще два примера умозаключений по схеме (II):

1. Растения (М) обогащают воздух кислородом (Р)

2. Деревья (S) – растения (М)

3. Деревья (S) обогащают воздух кислородом (Р)

 

1. Преступление (М) – общественно опасное деяние (Р)

2. Получение взятки (S) – преступление(М)

3. Получение взятки (S) – общественно опасное деяние (Р)

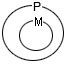
Причина, по которой эти умозаключения оказываются корректными, заключена в соотношений объемов их терминов, подставляемых на места параметров М, Р и S в формальной схеме вывода (II):

 

1. Все М суть Р:	2. Все S суть М:

Совместив эти две круговые схемы в одну, получаем:

Теперь наглядно убеждаемся, что при истинности любых по конкретному содержанию суждений-посылок, имеющих логическую форму «Все М есть Р» и «Все S есть М», обязательно истинным будет и суждение формы «Все S есть Р».

Полезно сопоставить алгебраическое уравнение а + b = b + a со схемой дедуктивного умозаключения. Как известно, это алгебраическое равенство сохраняется при любых конкретных числовых значениях переменных а и b: 4+3 =3+4, 5+6 = 6+5, и т.п. Аналогично, связь логических форм посылок с логической формой заключения в дедуктивных умозаключениях не зависит от конкретного содержания входящих в них суждений.

2.Достоверные (истинные) посылки индуктивного умозаключения обеспечивают лишь большую степень правдоподобия суждения, являющегося заключением, по сравнению с той, которую имело это суждение без учета посылок. Слыша гром и памятуя о том, что после удара молнии всегда раздается гром, мы индуктивно заключаем, что где-то был удар молнии. Однако гром мог иметь и иную причину (например, пушечный выстрел). Для индуктивных умозаключений как раз и характерна опора не только на логическую форму входящих суждений, но и на некоторые неформальные (содержательные) моменты (в нашем примере: «В мирное время пушки стреляют крайне редко»).

Следует сразу же отметить, что индуктивные умозаключения играют в мышлении ничуть не меньшую роль, чем дедуктивные. Если дедуктивные умозаключения позволяют систематизировать уже имеющееся знание, устанавливать логические связи «внутри» этого знания, применять общее знание к конкретным ситуациям, то индуктивные умозаключения участвуют при создании и обосновании гипотез, формировании нового знания. Возникает вопрос, как установить, что они выполняют эти функции? Наиболее простой способ состоит в следующем: если заключение получено из посылок по установленным наукой логикой правилам (логическим правилам), тогда такое умозаключение является корректным. В противном случае оно не является корректным. Правила эти таковы, что в дедуктивных выводах они гарантируют получение из истинных посылок истинного заключения, а в индуктивных – повышение степени правдоподобия суждения, являющегося заключением.