МЕТА РОБОТИ. Розрахунок і дослідження амплітудно-частотної та фазочастотної характеристик комплексного коефіцієнта передавання кіл
ЛАБОРАТОРНА РОБОТА №1
ДОСЛІДЖЕННЯ ЧАСТОТНИХ ХАРАКТЕРИСТИК
RC- І RL-КІЛ
Розрахунок і дослідження амплітудно-частотної та фазочастотної характеристик комплексного коефіцієнта передавання кіл, побудованих з RC або RL -елементів.
1.2 ТЕОРЕТИЧНІ ВІДОМОСТІ
Частотний аналіз лінійного ланцюга (аналіз в частотній області) – це аналіз ланцюга на дію у вигляді гармонійного коливання, що змінюється згідно із законом
або
Тут
f – циклічна частота, Гц=1/сек;
При дії на лінійний ланцюг гармонійним коливанням (1.1) струми і напруга в ланцюзі мінятимуться по аналогічному закону. Відбудеться зміна тільки амплітуд і початкових фаз, частота коливань не зміниться. Таким чином, завданням частотного аналізу ланцюга є знаходження амплітуд і початкових фаз струмів і напруги на елементах ланцюга для заданої частоти вхідної дії. Математичною основою частотного аналізу є метод комплексних амплітуд, відповідно до якого гармонійне коливання представляється в комплексній формі:
Тут
Зворотний перехід від символьного уявлення (1.2) до залежності від часу (1.1) проводиться по співвідношеннях:
Унаслідок лінійності перетворень по методу комплексних амплітуд має місце наступний зв'язок між математичними моделями R,C,L - елементів для часової і частотної областей:
Аналіз ланцюгів в частотній області проводиться по законах Кірхгофа і Ома, причому закон Ома для R,C,L – елементів записується у вигляді:
Тут Величини, зворотні реактивним опорам C,L – елементів, утворюють реактивну провідність: У загальному випадку ділянка ланцюга характеризується комплексним опором, що складається з активного R і реактивного X опорів, тобто Однією з основних характеристик чотирьохполюсників є комплексний коефіцієнт передачі по напрузі:
де Залежність модуля Частотні властивості чотирьохполюсників, складених з R,C або R,L – елементів, визначаються постійною часу ланцюга
|

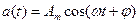 (1.1)
(1.1)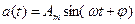 . (1.2)
. (1.2)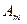 - амплітуда коливання;
- амплітуда коливання;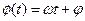 - фаза коливання;
- фаза коливання; - початкова фаза коливання (фаза при
- початкова фаза коливання (фаза при 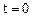 );
);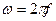 - кутова частота, рад/сек;
- кутова частота, рад/сек; - період коливань, сек.
- період коливань, сек.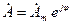 . (1.3)
. (1.3)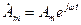 - комплексна амплітуда;
- комплексна амплітуда;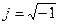 - уявна одиниця.
- уявна одиниця.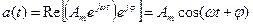 , (1.4)
, (1.4)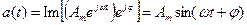 . (1.5)
. (1.5)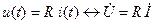 , (1.6)
, (1.6)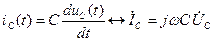 , (1.7)
, (1.7) . (1.8)
. (1.8)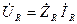 (1.9)
(1.9)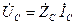 , (1.10)
, (1.10)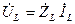 , (1.11)
, (1.11)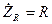 - активний опір;
- активний опір; 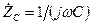 ,
, 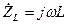 - реактивні опори.
- реактивні опори. ,
, 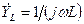 .
. . Цей опір можна представити в показовій формі:
. Цей опір можна представити в показовій формі: 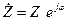 , де
, де  - модуль,
- модуль, 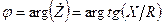 - аргумент комплексного числа.
- аргумент комплексного числа.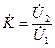 , (1.12)
, (1.12)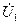 ,
, 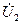 - комплексна напруга на вході і виході чотирьохполюсника, відповідно.
- комплексна напруга на вході і виході чотирьохполюсника, відповідно. комплексного коефіцієнта передачі від частоти називається амлитудно-частотною характеристикою (АЧХ) чотирьохполюсника, а залежність аргументу (фази)
комплексного коефіцієнта передачі від частоти називається амлитудно-частотною характеристикою (АЧХ) чотирьохполюсника, а залежність аргументу (фази) 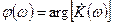 комплексного коефіцієнта передачі від частоти називається фазочастотною характеристикою (ФЧХ) чотирьохполюсника
комплексного коефіцієнта передачі від частоти називається фазочастотною характеристикою (ФЧХ) чотирьохполюсника або
або 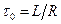 . На частоті зрізу
. На частоті зрізу 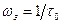 модуль коефіцієнта передачі зменшується в
модуль коефіцієнта передачі зменшується в 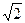 раз щодомаксимального значення, рівного одиниці. На основі R,C або R,L –ланцюгів складаються прості фільтри низьких частот (ФНЧ) або верхніх частот (ФВЧ). ФНЧ пропускає коливання низьких частот і затримує коливання високих частот. ФВЧ, навпаки, пропускає коливання високих частот і затримує коливання низьких частот. Частота зрізу
раз щодомаксимального значення, рівного одиниці. На основі R,C або R,L –ланцюгів складаються прості фільтри низьких частот (ФНЧ) або верхніх частот (ФВЧ). ФНЧ пропускає коливання низьких частот і затримує коливання високих частот. ФВЧ, навпаки, пропускає коливання високих частот і затримує коливання низьких частот. Частота зрізу 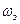 розділяє смуги пропускання і затримання.
розділяє смуги пропускання і затримання.


