Распределение Пуассона

Распределение Пуассона – это вариант биноминального распределения для случаев, когда вероятность альтернативных признаков неодинакова, один из них наблюдается чаще других, т.е. величина одной из вероятностей становится бесконечно малой, а число испытаний неограниченно возрастает.

Это распределение вероятностей называется распределением Пуассона, названного в честь крупнейшего французского математика и физика Симеона Дени Пуассона (1781-1840), который получил это распределение среди других, размышляя об отправлении правосудия в уголовных судах. По Лапласу, каждый из судей мог совершить ошибку с некоторой вероятностью. Вероятность того, что мнение судьи справедливо, в свою очередь неизвестная величина. Какое же значение ей приписать? По этому поводу Даллас в “Опыте философии теории вероятностей” пишет:
“Я предлагаю таким образом, что она может меняться от 1/2 до единицы, но что она не может быть ниже 1/2. Если бы это было не так, то решение имело бы столь же малое значение, как жребий; оно имеет цену постольку, поскольку мнение судьи более склонно к истине, чем к заблуждению. С помощью отношения числа голосов, благоприятствующих обвиняемому, к неблагоприятствующим, я определяю затем вероятность справедливости мнения судьи”.

Как видите, произвола здесь более чем достаточно. Пуассона это не устраивает, и он строит другую математическую модель суда присяжных. Пуассон отказался от наделения высказываний присяжных каким-либо распределением, получаемым умозрительно, и сказал, что вероятность правильного суждения должна оцениваться по статистическим данным. Однако основное предположение Пуассона – это предположение о независимости суждений отдельных присяжных.

Построив математическую модель голосования в суде присяжных, далее Пуассон “работает” уже только в этой модели, описываемой распределением Бернулли. Число присяжных равно двенадцати, и перед Пуассоном возникает задача решения уравнения двенадцатой степени относительно неизвестной вероятности правильного голосования.

Даже кубическое уравнение решить непросто, а уравнение степени выше четвертой решить в принятом в школе смысле, то есть в виде формулы, содержащей алгебраические действия, вообще нельзя. Вот здесь Пуассон и развивает общий метод для решения столь сложных уравнений, используя, конечно, специфику изучаемой модели.

Таким образом, успех Пуассона – следствие мощного исследования в рамках определенной математической модели. В то же время сама математическая модель, не адекватная изучаемому явлению – суду присяжных, хорошо описывает многие физические, технические, биологические явления, и именно это обеспечило бессмертие и ей, и ее автору.

Распределение Пуассона также исходит из биноминального распределения, когда величина одной из вероятностей р → 0, т.е. становится бесконечно малой, а число испытаний стремится к бесконечности, т.е. неограниченно возрастает. В таком случае произведение np → l стремится к некоторой малой, отличной от нуля величине. Тогда вероятность P (m) того, что в последователь-ности из n независимых испытаний некое редкое событие А с вероятностью P (A) ≠ 0 осуществится m раз, определена формулой

.

Значит, распределение Пуассона полностью описывается одним параметром λ;, который характеризует и среднее значение распределения, и меру разброса случайных значений.

Близким к этому закону является, например, статистическое распределение числа военнослу-жащих конных войск, погибших под копытами лошадей. При этом редкие события как бы уходят из класса событий слепого случая, приобретают вероятностное толкование.

Форма распределения Пуассона также существенно варьирует от крайней асимметрии к симметрии (в зависимости от величины λ;).

Основные свойства, рассмотренные выше, – положение на числовой оси, рассеивание, скошенность и выпуклость – в общем случае не определяют полностью аналитическое выражение для закона распределения некоторой случайной величины. Наоборот, аналитическое выражение, сообразующееся как с теоретическими знаниями о специфике случайной величины, так и с экспериментальными данными о ней, несет всю необходимую информацию о случайной величине, в том числе и об основных ее свойствах.
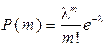