Применение основных законов распределения случайных величинЗадание №1. Техническая система состоит из пяти независимо друг от друга функционирующих узлов. Определите математическое ожидание, дисперсию, среднее квадратическое отклонение числа отказов узлов, если вероятность отказа любого из них равна 0,2. Методические указания по выполнению задания: Для биномиального распределения случайной величины Х числовые характеристики определяются следующим образом:
Задание №2 Определить вероятность того, что на АЗС находится один автомобиль, если среднее число автомобилей, находящихся в данном интервале времени на АЗС равно трем. Методические указания по выполнению задания: Применим закон Пуассона:
Задание №3 Среднее время обслуживания персонального компьютера 2 часа. Среднее квадратическое отклонение времени обслуживания 0,403ч. Определите вероятность окончания обслуживания ПК в течение интервала времени от 1,5 до 2,5 ч. Методические указания по выполнению задания: Данное распределение является нормальным (закон Гаусса).
По таблицам нормального распределения (приложение №1):
Задание №4 Случайная величина Х распределена по показательному закону Методические указания по выполнению задания: Тогда Задание №5 Троллейбусы прибывают на остановку через 4 минуты. Какова вероятность того, что время ожидания троллейбуса не превысит 3 минуты? Методические указания по выполнению задания: Так как
|
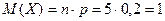
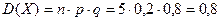
. Найти математическое ожидание, стандартное отклонение и дисперсию.
=5. Математическое ожидание М(Х) = стандартное отклонение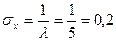 
. Дисперсия 
.
мин, а b-a=4 мин, то 
.
