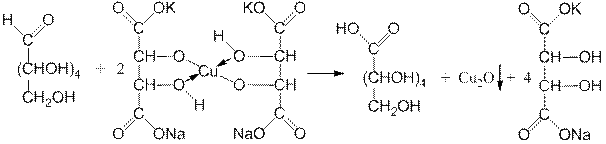
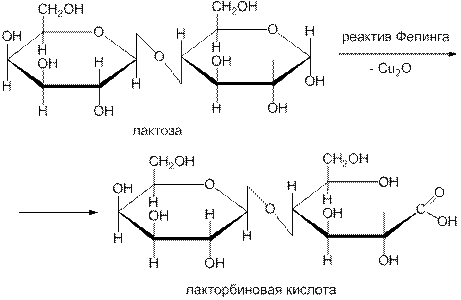
Взаимодействие сахаров с медновиннокислым комплексом (реактив Фелинга)
Реактивы и материалы: ü Исследуемый раствор – сок ü 5%-ный раствор глюкозы, лактозы, сахарозы ü Реактив Фелинга – смесь растворов А и Б: ü – раствор А: 4%-ный раствор сульфата меди, ü – раствор Б: щелочной раствор тартрата калия-натрия Методика проведения анализа Для приготовления реактива Фелинга в отдельной пробирке смешивают 10 капель расвора А и 10 капель раствора Б и используют в дальнейшей работе. В четыре пробирки наливают по 3 капли растворов сахаров – в первую – глюкозу, во вторую – лактозу, в третью – сахарозу, а в четвертую – 10 капель исследуемого раствора. Затем в каждую пробирку добавляют по 2 капли реактива Фелинга и нагревают их на водяной бане. Наблюдают выпадение оксида меди (I) Сu2О в пробирках с глюкозой и лактозой. В пробирке с сахарозой сохраняется синий цвет.
Восстанавливать соединения меди из реактива Фелинга при нагревании способны лишь те сахара, которые имеют в молекуле свободную альдегидную группу или гликозидный гидроксил.
Сахароза не восстанавливает раствор Фелинга, что указывает на отсутствие в ее молекуле свободной альдегидной группы.
|