Счисление в подвижной относительно Земли прямоугольной системе координат
При счислении в подвижной относительно Земли системе координат непосредственно определяется положение выбранного объекта F относительно ЛА. Пусть начало отсчета подвижной системы координат Охуz - на ЛА. Ось у направим вертикально вверх (рис. 6.3). Положение объекта F относительно ЛА определим вектором дальности Выразим скорость
где
Рис. 6.3. Относительное движение объекта
Рис. 6.4. Приведенная путевая скорость ЛА
Из уравнения (6.6) находим относительную скорость точки F:
Вектор
равен скорости движения ЛА (точки 0) относительно движущегося объекта F (рис. 6.4), которую называют приведенной путевой скоростью ЛА. Спроектируем равенство (6.7) на оси координат. Учитывая выражение (6.8), находим (6.9)
где Интегрируя первое и третье уравнения (6.9) по времени, получим формулы для счисления в подвижной системе прямоугольных координат
Для вычисления проекций
Рис. 6.5. Составляющие угловой скорости системы координат
Возможен и другой способ получения данных о проекции угловой скорости Во-вторых, при неизменном угле ǽ система отсчета Охуz в процессе движения ЛА над сфероидальной поверхностью Земли будет вращаться с дополнительной угловой скоростью
Производную ǽ можно определить путем дифференцирования угла ǽ, образованного осью х с плоскостью меридиана. Вследствие кривизны Земли система прямоугольных координат Охуz как было установлено в разд. 2, вращается вокруг оси, параллельной оси Земли (рис. 6.5), с угловой скоростью
где Wrop - горизонтальная составляющая путевой скорости; П - путевой угол; и вокруг оси, перпендикулярной плоскости меридиана, с угловой скоростью
Вектор угловой скорости
поэтому
Проектируя вектор Следует учитывать, что проекции При счислении координат в ограниченной области кривизну Земли можно не учитывать, считая
При таком допущении формулы (6.9) существенно упрощаются, причем отпадает необходимость определять широту Формулы упростятся еще больше, если систему отсчета ориентировать так, чтобы угол ǽ был постоянным, т.е. если перейти к невращающейся относительно вертикальной оси системе координат. В таком случае будем иметь Практически неподвижную прямоугольную систему координат целесообразно применять только для счисления в ограниченной области, в пределах которой можно не учитывать кривизну Земли.
|

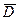 . В общем случае ЛА движется относительно Земли со скоростью
. В общем случае ЛА движется относительно Земли со скоростью 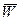 , а объект F - со скоростью
, а объект F - со скоростью 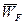 (рис. 6.3). Угловую скорость системы отсчета Охуz относительно Земли обозначим
(рис. 6.3). Угловую скорость системы отсчета Охуz относительно Земли обозначим 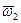 .
.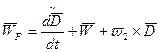 (6.6)
(6.6) - относительная (локальная) производная вектора
- относительная (локальная) производная вектора  ;
; - переносная скорость, возникающая вследствие вращения системы отсчета Охуz с угловой скоростью
- переносная скорость, возникающая вследствие вращения системы отсчета Охуz с угловой скоростью 

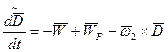 . (6.7)
. (6.7)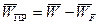 (6.8)
(6.8)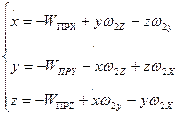
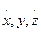 - проекции относительной скорости точки F на оси
- проекции относительной скорости точки F на оси 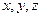 .
.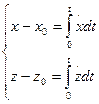 (6.10)
(6.10)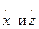 относительной скорости точки F необходимо располагать данными о проекциях угловой скорости
относительной скорости точки F необходимо располагать данными о проекциях угловой скорости 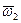 системы отсчета
системы отсчета 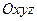 относительно Земли. Такие данные можно получить различными способами. Для этой цели можно применять двухстепенные гироскопы. Однако следует иметь в виду, что скоростные гироскопы обеспечивают измерение составляющих абсолютной угловой скорости. Чтобы получить значения составляющих
относительно Земли. Такие данные можно получить различными способами. Для этой цели можно применять двухстепенные гироскопы. Однако следует иметь в виду, что скоростные гироскопы обеспечивают измерение составляющих абсолютной угловой скорости. Чтобы получить значения составляющих 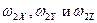 относительно угловой скорости
относительно угловой скорости 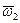 , необходимо, строго говоря, из показаний гироскопов вычесть значения проекций угловой скорости Земли на оси координат х, у, z. В противном случае будут иметь место методические ошибки, допустимость которых следует оценивать в каждом конкретном случае.
, необходимо, строго говоря, из показаний гироскопов вычесть значения проекций угловой скорости Земли на оси координат х, у, z. В противном случае будут иметь место методические ошибки, допустимость которых следует оценивать в каждом конкретном случае.
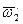 . Следовательно,
. Следовательно,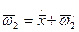

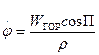
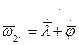
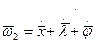 .
.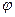 точки, в которой в данный момент находится ЛА. Это существенно усложняет решение задачи, так как при разложении вектора
точки, в которой в данный момент находится ЛА. Это существенно усложняет решение задачи, так как при разложении вектора 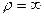 и
и 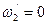 . В таком случае вектор
. В таком случае вектор  будет направлен в сторону, противоположную оси у. Поэтому
будет направлен в сторону, противоположную оси у. Поэтому 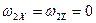 ,
, 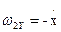
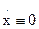 .
.


