В разомкнутых инерциальных системах в качестве исходных данных для счисления координат используются проекции путевой скорости 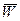 на взаимно перпендикулярные оси, например на оси х, у,z системы отсчета Охуz. Необходимые исходные данные получают с помощью интегрирования составляющих относительного ускорения
на взаимно перпендикулярные оси, например на оси х, у,z системы отсчета Охуz. Необходимые исходные данные получают с помощью интегрирования составляющих относительного ускорения
 ,
,  ,
, 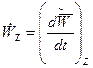 .
.
Где 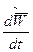 - локальная (относительная) производная вектора, равная скорости его конца относительно вращающейся системы отсчета Охуz.
- локальная (относительная) производная вектора, равная скорости его конца относительно вращающейся системы отсчета Охуz.
Значения 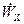 ,
,  и
и  находят по показаниям акселерометров, оси чувствительности которых совпадают с осями координат х,у,z.
находят по показаниям акселерометров, оси чувствительности которых совпадают с осями координат х,у,z.
Показания каждого из акселерометров выражаются формулами, подобными формуле (6.17)._
Обозначим вектором S результирующие показания всех трех акселерометров. Тогда, по аналогии с формулой (6.17), можем записать
 (6.18)
(6.18)
где  - гравитационное ускорение;
- гравитационное ускорение; 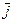 - абсолютное ускорение центральной точки корпуса акселерометра.
- абсолютное ускорение центральной точки корпуса акселерометра.
Но абсолютное ускорение
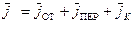 (6.19)
(6.19)
где  - относительное ускорение центральной точки корпуса акселерометра;
- относительное ускорение центральной точки корпуса акселерометра;  - переносное ускорение;
- переносное ускорение;  - кориолисово ускорение.
- кориолисово ускорение.
В рассматриваемом случае относительным движением является движение ЛА относительно Земли со скоростью 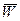 , равной его путевой скорости. Поэтому
, равной его путевой скорости. Поэтому
 ,
, 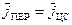 ,
, 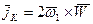
где 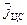 - центростремительное ускорение, возникающее при вращении Земли;
- центростремительное ускорение, возникающее при вращении Земли;  - угловая скорость Земли.
- угловая скорость Земли.
Учитывая, что система отсчета Охуz вращается относительно Земли с угловой скоростью  , представим производную
, представим производную 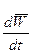 виде
виде
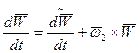
где 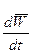 - скорость конца вектора
- скорость конца вектора 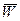 относительно Земли;
относительно Земли; 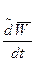 -локальная (относительная) производная вектора
-локальная (относительная) производная вектора 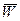 , равная скорости его конца относительно вращающейся системы отсчета Охуz;
, равная скорости его конца относительно вращающейся системы отсчета Охуz; 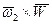 - скорость конца вектора
- скорость конца вектора 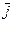 , возникающая при его вращении совместно с системой отсчета Охуz.
, возникающая при его вращении совместно с системой отсчета Охуz.
Подставим значение абсолютного ускорения j и входящих в его выражение отдельных членов в равенство (6.18). Получим
 (6.20)
(6.20)
Решим последнее равенство относительно 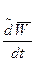 Замечая, что
Замечая, что
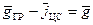
где  - ускорение свободного падения, находим
- ускорение свободного падения, находим
 (6.21)
(6.21)
где 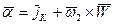
Проектируя равенство (6.21) на оси х,у,z, получаем
 (6.23)
(6.23)
где
 (6.24)
(6.24)
После интегрирования равенств (6.23) по времени имеем
 (6.25)
(6.25)
Из равенств (6.25) видно, что интегрирование показаний акселерометров позволяет определить значения проекций путевой скорости 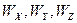 используемые при счислении координат, с ошибками
используемые при счислении координат, с ошибками
 (6.26)
(6.26)
Члены  в выражениях ошибок можно исключить, если обеспечить горизонтальное положение осей чувствительности х и z двух акселерометров. Для этого следует уравновесить акселерометры на стабилизированной платформе, например на силовой гироскопической платформе. Тогда при строго горизонтальном положении осей x и z и вертикальном расположении третьей оси будем иметь
в выражениях ошибок можно исключить, если обеспечить горизонтальное положение осей чувствительности х и z двух акселерометров. Для этого следует уравновесить акселерометры на стабилизированной платформе, например на силовой гироскопической платформе. Тогда при строго горизонтальном положении осей x и z и вертикальном расположении третьей оси будем иметь 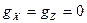 ,
, 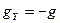 .
.
Значение 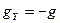 можно учесть, вводя поправку в показания соответствующего акселерометра.
можно учесть, вводя поправку в показания соответствующего акселерометра.
Но практически установить платформу с акселерометрами строго горизонтально невозможно. Поэтому в формулах (6.25) и (6.26) члены  не могут быть полностью исключены. Это приведет к ошибкам в определении проекции путевой скорости на горизонтальные оси.
не могут быть полностью исключены. Это приведет к ошибкам в определении проекции путевой скорости на горизонтальные оси.
Допустим, например, что относительно оси z платформа выставлена с ошибкой 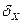 . в таком случае при малом угле
. в таком случае при малом угле 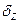 приближенно будем иметь
приближенно будем иметь 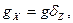
Наличие составляющей 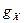 ускорения свободного падения приведет к ошибке в определении проекции
ускорения свободного падения приведет к ошибке в определении проекции 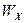 путевой скорости на ось х. Положим, например, что угол
путевой скорости на ось х. Положим, например, что угол 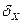 изменяется по следующему закону:
изменяется по следующему закону: 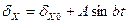
Тогда ошибка в определении 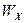 будет равна
будет равна
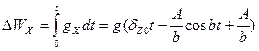
ошибка в счислении координаты X составит
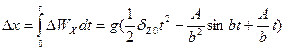
При синусоидальных колебаниях силовой гироскопической платформы амплитуда колебательной части ошибок возрастает с уменьшением угловой частоты в колебаний платформы.
Постоянная составляющая 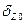 ошибки в установке платформы приводит к накоплению ошибки в путевой скорости по линейному закону, а в счисляемой координате - по квадратичному закону.
ошибки в установке платформы приводит к накоплению ошибки в путевой скорости по линейному закону, а в счисляемой координате - по квадратичному закону.

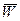 на взаимно перпендикулярные оси, например на оси х, у,z системы отсчета Охуz. Необходимые исходные данные получают с помощью интегрирования составляющих относительного ускорения
на взаимно перпендикулярные оси, например на оси х, у,z системы отсчета Охуz. Необходимые исходные данные получают с помощью интегрирования составляющих относительного ускорения ,
,  ,
, 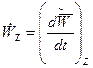 .
.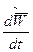 - локальная (относительная) производная вектора, равная скорости его конца относительно вращающейся системы отсчета Охуz.
- локальная (относительная) производная вектора, равная скорости его конца относительно вращающейся системы отсчета Охуz.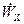 ,
,  и
и  находят по показаниям акселерометров, оси чувствительности которых совпадают с осями координат х,у,z.
находят по показаниям акселерометров, оси чувствительности которых совпадают с осями координат х,у,z. (6.18)
(6.18) - гравитационное ускорение;
- гравитационное ускорение; 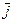 - абсолютное ускорение центральной точки корпуса акселерометра.
- абсолютное ускорение центральной точки корпуса акселерометра.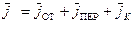 (6.19)
(6.19) - относительное ускорение центральной точки корпуса акселерометра;
- относительное ускорение центральной точки корпуса акселерометра;  - переносное ускорение;
- переносное ускорение;  - кориолисово ускорение.
- кориолисово ускорение. ,
, 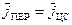 ,
, 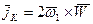
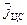 - центростремительное ускорение, возникающее при вращении Земли;
- центростремительное ускорение, возникающее при вращении Земли;  - угловая скорость Земли.
- угловая скорость Земли. , представим производную
, представим производную 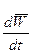 виде
виде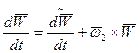
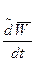 -локальная (относительная) производная вектора
-локальная (относительная) производная вектора 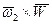 - скорость конца вектора
- скорость конца вектора 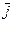 , возникающая при его вращении совместно с системой отсчета Охуz.
, возникающая при его вращении совместно с системой отсчета Охуz. (6.20)
(6.20)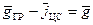
 - ускорение свободного падения, находим
- ускорение свободного падения, находим (6.21)
(6.21)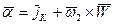
 (6.23)
(6.23) (6.24)
(6.24) (6.25)
(6.25)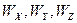 используемые при счислении координат, с ошибками
используемые при счислении координат, с ошибками (6.26)
(6.26) в выражениях ошибок можно исключить, если обеспечить горизонтальное положение осей чувствительности х и z двух акселерометров. Для этого следует уравновесить акселерометры на стабилизированной платформе, например на силовой гироскопической платформе. Тогда при строго горизонтальном положении осей x и z и вертикальном расположении третьей оси будем иметь
в выражениях ошибок можно исключить, если обеспечить горизонтальное положение осей чувствительности х и z двух акселерометров. Для этого следует уравновесить акселерометры на стабилизированной платформе, например на силовой гироскопической платформе. Тогда при строго горизонтальном положении осей x и z и вертикальном расположении третьей оси будем иметь 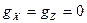 ,
, 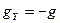 .
.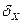 . в таком случае при малом угле
. в таком случае при малом угле 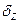 приближенно будем иметь
приближенно будем иметь 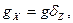
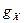 ускорения свободного падения приведет к ошибке в определении проекции
ускорения свободного падения приведет к ошибке в определении проекции 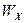 путевой скорости на ось х. Положим, например, что угол
путевой скорости на ось х. Положим, например, что угол 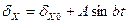
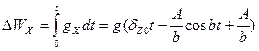
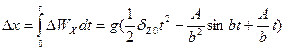
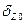 ошибки в установке платформы приводит к накоплению ошибки в путевой скорости по линейному закону, а в счисляемой координате - по квадратичному закону.
ошибки в установке платформы приводит к накоплению ошибки в путевой скорости по линейному закону, а в счисляемой координате - по квадратичному закону.


