Принцип работы замкнутой инерциальной системы счисления координат
В замкнутой инерциальной системе счисления координат два акселерометра с взаимно перпендикулярными осями чувствительности устанавливаются на общей платформе. Оси чувствительности акселерометров совпадают с осями x и у системы координат Охуz (рис. 6.10). Платформа устанавливается так, чтобы оси чувствительности акселерометров лежали в плоскости геоцентрического горизонта, а нормаль к платформе, совпадающая с осью y, проходила через центр Земли. Ось х располагается под некоторым углом ǽ относительно плоскости меридиана. При движении точки 0 относительно Земли показания акселерометров Замкнутая инерциальная система счисления координат обеспечивает решение следующих задач. По направлению оси у относительно Земли она позволяет определить направление вертикали в точке, которая в данный момент совпадает с точкой 0. По изменению направления осей чувствительности акселерометров относительно начального положения она позволяет определить координаты точки 0. Замкнутая инерциальная система счисления координат дает возможность определить путевую скорость и путевой угол ЛА, измерить курс, углы крена и тангажа с более высокой точностью, чем с помощью гировертикали.
Рис. 6.10. Ориентация осей чувствительности акселерометров в замкнутой инерциальной системе счисления координат
Недостаток замкнутой инерциальной системы счисления координат состоит в сложности ее устройства и эксплуатации, в высоких требованиях, предъявляемых к точности ее изготовления. На рис. 6.11 приведена кинематическая схема конструкции замкнутой инерциальной системы счисления координат. Акселерометры К гироскопам ЛА (точка 0,его центр массы) движется по окружности,плоскость которой сохраняет неизменное положение в инерциальном пространстве, а центр совпадает с центром Земли (рис. 6.12). Центр массы ЛА на окружности определяется полярным углом
Необходимо в начальный момент платформу с акселерометром установить так, чтобы ось чувствительности акселерометра была направлена по касательной к окружности. В процессе движения точки О по окружности платформу с акселерометром необходимо, вращать с угловой скоростью
где Vр - трансверсальная составляющая скорости точки 0, равная в данном случае абсолютной скорости этой точки. Значение угловой скорости W определяется путем обработки и змернного ускорения. Между показаниями акселерометра
Угловую скорость
С помощью поправки С вводятся поправки к показаниям акселерометра. Коэффициент n и поправку С можно определить из следующего условия, вытекающего из равенств (6.27) и (6.29):
Продифференцируем уравнение (6.30) по времени. Имея в данном случае
Показания акселерометра
После подстановки этих значений в формулу (6.31) получим
Поправку С и коэффициент n необходимо выбрать так, чтобы удовлетворялось равенство (6.32), причем
Тогда из уравнения (6.32) исключается неизвестное ускорение Vр. Поправка Если в рассмотренном случае учитывать найденные значения Изменение полярного угла Замкнутая инерциальная система счисления координат дает возможность определить положение центра массы ЛА на окружности по углу поворота платформы относительно фиксированного начала отсчета. Ошибка в определении направления вертикали, возникающая вследствие погрешностей в значении угловой скорости Допустим, что в течение некоторого промежутка времени платформа вращалась с угловой скоростью
Рис. 6.13. Ошибка инерциальной вертикали Анализ уравнений движения платформы с акселерометром показывает, что платформа, а вместе с нею и инерциальная вертикаль будут колебаться около положения равновесия с периодом Рассмотренное свойство замкнутой инерциальной системы счисления координат дает возможность с высокой точность определять направление геоцентрической вертикали. Точность, с которой вычисляется положение ЛА, зависит от точности определения направления геоцентрической вертикали и от точности фиксации начала отсчета
|

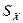 и
и  обрабатываются, после чего платформа приводится во вращение вокруг осей чувствительности x и z. Скорость вращения платформы должна быть такова, чтобы оси чувствительности акселерометров x и z все время оставались в плоскости геоцентрического горизонта, а нормаль к платформе все время проходила через центр Земли.
обрабатываются, после чего платформа приводится во вращение вокруг осей чувствительности x и z. Скорость вращения платформы должна быть такова, чтобы оси чувствительности акселерометров x и z все время оставались в плоскости геоцентрического горизонта, а нормаль к платформе все время проходила через центр Земли.
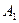 и
и  , оси чувствительности которых параллельны осям х и у системы отсчета Оxyz, установлены на трехкомпонентной гироскопической платформе. Одновременно ось x является осью чувствительности гироскопа
, оси чувствительности которых параллельны осям х и у системы отсчета Оxyz, установлены на трехкомпонентной гироскопической платформе. Одновременно ось x является осью чувствительности гироскопа  , а ось z - осью чувствительности гироскопа
, а ось z - осью чувствительности гироскопа 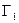 . Ось чувствительности третьего, азимутального гироскопа (АГ) параллельна оси у.
. Ось чувствительности третьего, азимутального гироскопа (АГ) параллельна оси у.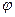 . Угловая скорость точки 0 вычисляется путем обработки трансеерсальной составляющей ускорения, нормальной к радиусу-вектору
. Угловая скорость точки 0 вычисляется путем обработки трансеерсальной составляющей ускорения, нормальной к радиусу-вектору  точки 0. Ось чувствительности акселерометра, предназначенного.для измерения угловой скорости точки 0, должна совпадать с нормалью к радиусу-вектору точки 0 (на рис. 6.12 ось чувствительности акселерометра совмещена с осью x).
точки 0. Ось чувствительности акселерометра, предназначенного.для измерения угловой скорости точки 0, должна совпадать с нормалью к радиусу-вектору точки 0 (на рис. 6.12 ось чувствительности акселерометра совмещена с осью x).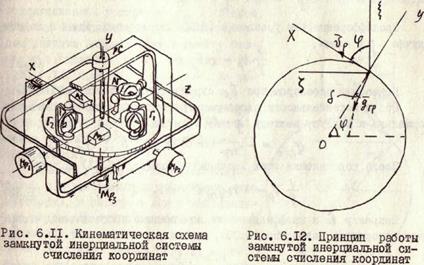
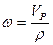 (6.27)
(6.27)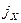 существует линейная зависимость:
существует линейная зависимость: (6.28)
(6.28) находят по формуле
находят по формуле (6.29)
(6.29) (6.30)
(6.30)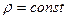
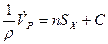 (6.31)
(6.31) . Тогда
. Тогда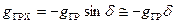 ,
, 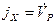 .
. (6.32)
(6.32)
 .
. .
. .
. . Тогда накопится ошибка (рис. 6.13)
. Тогда накопится ошибка (рис. 6.13) 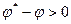 . На ось х будет проектироваться гравитационное ускорение
. На ось х будет проектироваться гравитационное ускорение 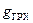 , которое, в целях наглядности и простоты, мы будем считать направленным к центру Земли, т.е. положим
, которое, в целях наглядности и простоты, мы будем считать направленным к центру Земли, т.е. положим  . Как видно из рис. 6.12, проекция
. Как видно из рис. 6.12, проекция  . Из равенств (6.17) и (6.33) следует, что угловая скорость платформы начнет при этом убывать, вследствие чего накопление ошибки
. Из равенств (6.17) и (6.33) следует, что угловая скорость платформы начнет при этом убывать, вследствие чего накопление ошибки  постепенно прекратится.
постепенно прекратится.
 мин, равным периоду колебаний математического маятника, длина нити которого равна радиусу Земли.
мин, равным периоду колебаний математического маятника, длина нити которого равна радиусу Земли.


