Функція Лагранжа і закони збереження.
В § 13 ми дали формальне визначення (13.19) функції Лагранжа. Тут ми покажемо, що функція Лагранжа має глибокий фізичний зміст – вона є найважливіша характеристична функція механічної системи, що містить у собі величезну фізичну інформацію про стан системи в довільний момент часу. Щоб переконатися в цьому, досить показати, що вже по зовнішньому вигляді функції Лагранжа досить просто відшукати закони збереження, тобто такі найважливіші перші інтеграли рівнянь Лагранжа, які пов’язані із симетріями простору й часу (або зовнішнього силового поля) і накладених на систему в'язів (див. р. 2). Розглянемо механічну систему, функція Лагранжа якої явно від часу не залежить, тобто Для цього записуємо повну похідну по часом від
Заміняючи тут
або
З (14.1) видно, що якщо
називана повною механічною енергією. Умову консервативності системи Нове (у порівнянню з даним в § 9) визначення (14.2) повної енергії є більш загальним (тому перший інтеграл руху (14.2) іноді називають законом збереження узагальненої енергії), але у всіх випадках, коли можна користуватися поняттям повної потенціальної енергії, визначення (14.2) збігається зі звичайним визначенням повної енергії як суми кінетичної й потенціальної енергій. Наприклад, для системи, на яку діють тільки потенційні сили, функція Лагранжа має вигляд (13.29), при цьому згідно (13.32):
і, отже, повна енергія (14.2) дорівнює:
і, отже, повна енергія (14.2) дорівнює:
тобто в цьому випадку з повної енергії (14.2) обов'язково випадає лінійний по узагальнених швидкостях член Розглянемо тепер питання про зв'язок виду функції Лагранжа із законами збереження імпульсу й моменту імпульсу системи (див. §§ 10-11). При цьому варто врахувати, що використовуючи «мову» узагальнених координат потрібно вживати поняття узагальнених імпульсів, тобто деяких узагальнень звичайних понять імпульсу й моменту імпульсу. Тому дамо спочатку відповідне визначення. Узагальненими імпульсами
Якщо узагальнена координата Природно, що структура узагальнених імпульсів невільної системи виявляється більш складною в порівнянні з виразами для імпульсу й моменту імпульсу (див. § 3) вільної системи. Наприклад, для системи, описуваною функцією Лагранжа (13.29),
Використовуючи поняття узагальненого імпульсу (14.3), рівняння Лагранжа (13.18) можна переписати у вигляді:
Нерідко трапляється так, що деякі з
Помітимо, що циклічність деякої координати
Дійсно, якщо У свою чергу, інваріантність Звідси випливає методична рекомендація: хоча набори узагальнених координат, пов'язаних між собою точковими перетвореннями (13.14), теоретично рівноправні, однак для спрощення рішень конкретних задач механіки методом Лагранжа узагальнені координати системи варто вибирати з урахуванням симетрії задачі; тільки в цьому випадку окремі Т. ч., функція Лагранжа дійсно є найважливішою функцією стану механічної системи: знання явного вигляду
§ 15. Основна задача варіаційного числення. Рівняння Ейлера.
З метою подальшого розвитку методу Лагранжа в цьому параграфі ми попередньо познайомимося з деякими елементами варіаційного числення – спеціального розділу математики, що займається дослідженням екстремальних властивостей криволінійних інтегралів, що залежать від вибору однієї або декількох функцій (такі криволінійні інтеграли називають функціоналами). Найпростішим функціоналом є криволінійний інтеграл:
залежний від вибору однієї функції Основна задача варіаційного числення (у застосуванні до (15.1)) складається в знаходженні такої функції
де Найпростіший шлях розв’язок поставленої задачі полягає в наступному. Допустимо, що задача вирішена і функція
де
і Підстановка (15.3) в (15.1) приводить до деякої допоміжної функції параметра
Тим самим задача знаходження екстремуму функціонала (15.1) звелася до дослідження на екстремум функції однієї змінної Обчислимо спочатку похідну
Інтегруючи другий інтеграл у правій частині (15.6) по частинам з урахуванням граничних умов (15.4) одержуємо:
З врахуванням (15.7) перепишемо (15.6) у вигляді:
звідки умова екстремуму
де ми врахували, що Так як
Рівність (15.9) називається рівнянням Ейлера. Так як функція
|

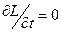 ; допустимо також, що на систему не діють дисипативні сили. Покажемо, що цієї інформації досить для одержання закону збереження повної енергії зазначеної системи.
; допустимо також, що на систему не діють дисипативні сили. Покажемо, що цієї інформації досить для одержання закону збереження повної енергії зазначеної системи. :
: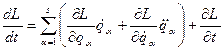 .
.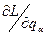 відповідно з (13.18) на
відповідно з (13.18) на 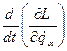 , одержуємо:
, одержуємо: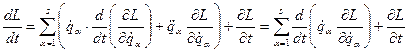
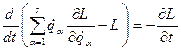 . (14.1)
. (14.1)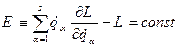 , (14.2)
, (14.2) (див. § 9). Фізично ця вимога є наслідком виконання двох умов: 1) однорідності часу для замкнутих систем (або незалежності від часу зовнішніх силових полів); 2) стаціонарності в'язів, накладених на систему.
(див. § 9). Фізично ця вимога є наслідком виконання двох умов: 1) однорідності часу для замкнутих систем (або незалежності від часу зовнішніх силових полів); 2) стаціонарності в'язів, накладених на систему.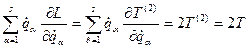
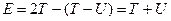 . Розглянемо ще один приклад консервативної системи (для який
. Розглянемо ще один приклад консервативної системи (для який 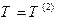 ) з узагальнено-потенційними силами, узагальнений потенціал
) з узагальнено-потенційними силами, узагальнений потенціал 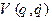 якої можна представити у вигляді суми
якої можна представити у вигляді суми 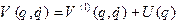 , де
, де 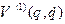 - однорідналінійна функція узагальнених швидкостей
- однорідналінійна функція узагальнених швидкостей 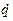 , і
, і 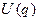 - звичайна потенціальна енергія, що залежить тільки від узагальнених координат
- звичайна потенціальна енергія, що залежить тільки від узагальнених координат 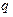 . У цьому випадку, згідно (13.30)
. У цьому випадку, згідно (13.30)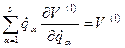 і:
і: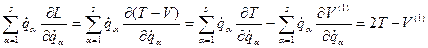
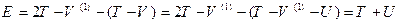 ,
,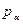 механічної системи називають скалярні величини, які визначаються формулою:
механічної системи називають скалярні величини, які визначаються формулою: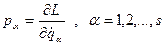 , (14.3)
, (14.3)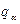 має розмірність довжини, то відповідний їй узагальнений імпульс
має розмірність довжини, то відповідний їй узагальнений імпульс  . (14.4)
. (14.4)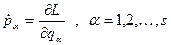 . (14.5)
. (14.5)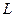 явно не входять (а входять лише їхні похідні по часом
явно не входять (а входять лише їхні похідні по часом 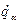 ); такі
); такі 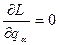 . Тоді з (14.5) одержуємо наступний закон збереження: якщо узагальнена координата
. Тоді з (14.5) одержуємо наступний закон збереження: якщо узагальнена координата 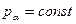 , якщо
, якщо 
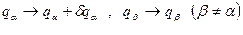 . (14.7)
. (14.7)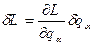 , обумовлене цими перетвореннями, повинне обертатися в нуль, тобто
, обумовлене цими перетвореннями, повинне обертатися в нуль, тобто 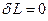 , що еквівалентно вимозі
, що еквівалентно вимозі 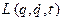 дозволяє не тільки скласти рівняння руху для систем з потенційними й узагальнено-потенційними активними силами, але й одержати закони збереження для таких систем.
дозволяє не тільки скласти рівняння руху для систем з потенційними й узагальнено-потенційними активними силами, але й одержати закони збереження для таких систем.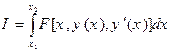 , (15.1)
, (15.1)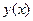 . Тут
. Тут 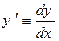 .
. , (15.2)
, (15.2) ,
,  – наперед задані величини.
– наперед задані величини. , близьку до
, близьку до 
 , (15.3)
, (15.3) - довільна функція, що задовольняє таким граничним умовам щоб
- довільна функція, що задовольняє таким граничним умовам щоб  , (15.4)
, (15.4)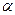 - малий чисельний параметр.
- малий чисельний параметр. . (15.5)
. (15.5)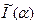 . А для цього, як відомо, необхідно знайти значення похідної
. А для цього, як відомо, необхідно знайти значення похідної 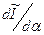 при
при 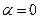 й прирівняти його нулю (при цьому екстремум функціоналові (15.1) забезпечує по нашому припущенню функція
й прирівняти його нулю (при цьому екстремум функціоналові (15.1) забезпечує по нашому припущенню функція 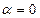 ).
).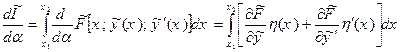 . (15.6)
. (15.6)
 . (15.7)
. (15.7)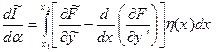 ,
, , а, отже, і функціонала I запишеться у вигляді:
, а, отже, і функціонала I запишеться у вигляді: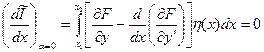 , (15.8)
, (15.8) й
й 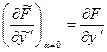 .
.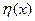 - довільна функція, то ми дійдемо висновку, що рівність (15.8) має місце тільки в тому випадку, якщо коефіцієнт, що міститься перед
- довільна функція, то ми дійдемо висновку, що рівність (15.8) має місце тільки в тому випадку, якщо коефіцієнт, що міститься перед 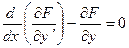 . (15.9)
. (15.9) містить першу похідну
містить першу похідну 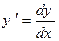 , то ліва частина (15.9) буде містити другу похідну
, то ліва частина (15.9) буде містити другу похідну 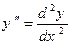 , тому рівняння Ейлера є звичайним диференціальним рівнянням другого порядку відносно шуканої функції
, тому рівняння Ейлера є звичайним диференціальним рівнянням другого порядку відносно шуканої функції 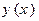 , і, отже, загальне розв’язок рівняння (15.9) містить дві довільні сталі, які визначаються граничними умовами (15.2). Т. ч., ми довели, що функція
, і, отже, загальне розв’язок рівняння (15.9) містить дві довільні сталі, які визначаються граничними умовами (15.2). Т. ч., ми довели, що функція 


