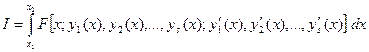 , (15.10)
, (15.10)
залежного від S незалежних функцій 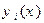 й їхніх похідних
й їхніх похідних  . Основна варіаційна задача в застосуванні до (15.10) складається в знаходженні такого набору функцій
. Основна варіаційна задача в застосуванні до (15.10) складається в знаходженні такого набору функцій 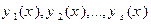 , які: 1) реалізують екстремум функціонала (15.10) і 2) задовольняють граничним умовам:
, які: 1) реалізують екстремум функціонала (15.10) і 2) задовольняють граничним умовам:
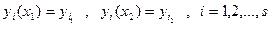 , (15.11)
, (15.11)
де 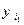 ,
, 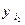 - задані величини.
- задані величини.
У повній аналогії з попереднім, будуємо нові функції 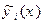 , близькі до
, близькі до 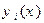 :
:
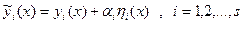 , (15.12)
, (15.12)
де 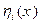 - довільні функції, що задовольняють граничним умовам:
- довільні функції, що задовольняють граничним умовам:
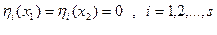 , (15.13)
, (15.13)
і 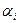 - малі чисельні параметри. Зводимо задачу до відшукання екстремуму функції:
- малі чисельні параметри. Зводимо задачу до відшукання екстремуму функції:
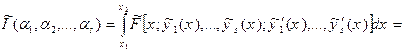
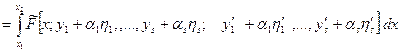 . (15.14)
. (15.14)
Умову екстремуму функції (15.14) можна записати у вигляді:
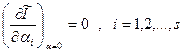 , (15.15)
, (15.15)
де ми позначимо 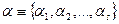 . Множачи кожне i- ту рівність (15.15) на
. Множачи кожне i- ту рівність (15.15) на 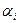 й складаючи отримані результати почленно, одержуємо наступний еквівалентний запис умови екстремуму у вигляді одного рівняння:
й складаючи отримані результати почленно, одержуємо наступний еквівалентний запис умови екстремуму у вигляді одного рівняння:
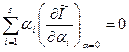 . (15.16)
. (15.16)
Підставляючи сюди (15.14) і використовуючи правило диференціювання інтеграла по параметру, перепишемо (15.16) у такий спосіб:
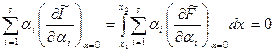 (15.17)
(15.17)
Для підінтегральної функції в лівій частині (15.17) маємо:
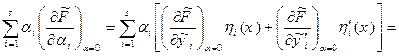
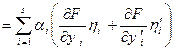 . (15.18)
. (15.18)
Підставляючи (15.18) в (15.17) і інтегруючи другий інтеграл по частинам з урахуванням граничних умов (15.13), одержуємо:
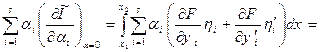
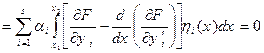 . (15.19)
. (15.19)
В силу дозвілля свободи функцій 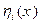 з (15.19) випливає висновок: функції
з (15.19) випливає висновок: функції  , що реалізують екстремум функціонала (15.10), повинні задовольняти системі рівнянь Ейлера:
, що реалізують екстремум функціонала (15.10), повинні задовольняти системі рівнянь Ейлера:
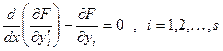 . (15.20)
. (15.20)
Отримані результати можна сформулювати в трохи іншому (еквівалентному) вигляді, якщо скористатися поняттям варіації функції й варіації функціонала. У повній відповідності з визначенням варіації функції в § 12, ми визначаємо варіації 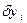 функцій
функцій  згідно (15.12) у такий спосіб:
згідно (15.12) у такий спосіб:
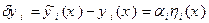 . (15.21)
. (15.21)
Варіювання будь-якої функції  спричиняє варіювання і її похідної
спричиняє варіювання і її похідної 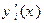 ; варіацію
; варіацію 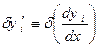 ми згідно (15.14) визначаємо формулою:
ми згідно (15.14) визначаємо формулою:
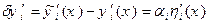 (15.22)
(15.22)
З визначень (15.21) і (15.22) випливає важливе правило обчислення варіацій: операції варіювання й диференціювання можна переміщувати, тобто:
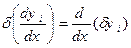 . (15.23)
. (15.23)
Дійсно, диференціюючи по 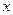 рівність (15.21)
рівність (15.21)
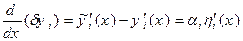 ,
,
і порівнюючи цей результат з (15.22), одержуємо (15.23).
У результаті варіювання функцій  й їхніх похідних
й їхніх похідних 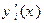 одержує приріст і будь-яка функція виду
одержує приріст і будь-яка функція виду 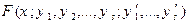 ; варіацією
; варіацією 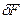 функції
функції 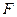 називається лінійна по
називається лінійна по  й
й 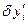 частина приросту
частина приросту 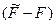 цієї функції, тобто:
цієї функції, тобто:
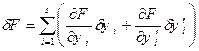 . (15.24)
. (15.24)
(Для одержання (15.24) потрібно розкласти 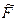 в ряд по
в ряд по 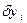 й
й  й обмежитися для
й обмежитися для 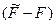 першим не зникаючим доданком).
першим не зникаючим доданком).
Нагадаємо, що відповідно до (15.14), 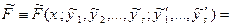
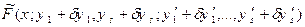 . Праві частини рівностей (15.24) і (15.18) рівні (з врахуванням (15.21) і (15.22)), тому формула:
. Праві частини рівностей (15.24) і (15.18) рівні (з врахуванням (15.21) і (15.22)), тому формула:
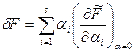 (15.25)
(15.25)
дає еквівалентне (15.24) визначення варіації функції 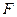 .
.
За аналогією з (15.25), першою варіацією функціонала (15.10) або просто варіацією функціонала (15.10) називають величину 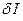 , обумовлену вираженням:
, обумовлену вираженням:
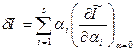 (15.26)
(15.26)
Визначення (15.26) дозволяє переписати результат (15.19) у вигляді:
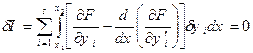 . (15.27)
. (15.27)
Тим самим ми одержали інше формулювання результату розв’язку основної варіаційної задачі: функції  ,
, 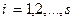 , що реалізують екстремум функціонала (15.10), повинні перетворювати в нуль варіацію функціонала
, що реалізують екстремум функціонала (15.10), повинні перетворювати в нуль варіацію функціонала 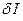 . Це твердження, як видно з (15.27), рівносильні вимозі (15.20); дійсно, так як функції
. Це твердження, як видно з (15.27), рівносильні вимозі (15.20); дійсно, так як функції  незалежні, то
незалежні, то  також незалежні й, отже, довільні, тому рівність
також незалежні й, отже, довільні, тому рівність 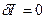 має місце тільки при виконанні рівнянь Ейлера (15.20).
має місце тільки при виконанні рівнянь Ейлера (15.20).
Визначення (15.25) і (15.26) дозволяють «витягти» з (15.17) важливе правило: операції варіювання й інтегрування можна міняти місцями, тобто:
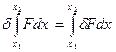 . (15.28)
. (15.28)
Зауваження. За аналогією з визначенням 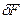 (15.24) можна дати інше (еквівалентне (15.26)) визначення першої варіації функціонала: варіацією
(15.24) можна дати інше (еквівалентне (15.26)) визначення першої варіації функціонала: варіацією 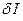 функціонала (15.10) називається лінійна (головна) частина приросту:
функціонала (15.10) називається лінійна (головна) частина приросту:
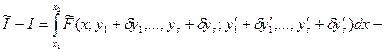
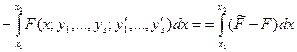 , (15.29)
, (15.29)
яке одержує функціонал 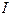 внаслідок варіації функцій
внаслідок варіації функцій  й їхніх похідних
й їхніх похідних 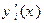 у підінтегральному виразі (відзначимо тут, що у фізичній літературі іноді варіацією
у підінтегральному виразі (відзначимо тут, що у фізичній літературі іноді варіацією 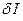 називають саме приріст (15.29), тобто величину
називають саме приріст (15.29), тобто величину 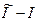 , що математично некоректно). Для одержання явного виразу для
, що математично некоректно). Для одержання явного виразу для 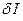 розкладемо функцію
розкладемо функцію 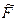 в (15.29) у ряд по ступенях
в (15.29) у ряд по ступенях 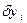 й
й  й обмежимося в цьому розкладанні тільки членами першого порядку малості (тим самим ми і одержуємо лінійну частину різниці
й обмежимося в цьому розкладанні тільки членами першого порядку малості (тим самим ми і одержуємо лінійну частину різниці 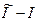 ):
):

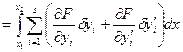 . (15.30)
. (15.30)
З огляду на визначення 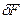 (15.24) і (15.25), дійдемо висновку, що визначення варіації функціонала (15.30) еквівалентно визначенню (15.26). Помітимо, що визначення (15.30) з врахуванням (15.24) фактично збігається із властивістю операції варіювання (15.28).
(15.24) і (15.25), дійдемо висновку, що визначення варіації функціонала (15.30) еквівалентно визначенню (15.26). Помітимо, що визначення (15.30) з врахуванням (15.24) фактично збігається із властивістю операції варіювання (15.28).
§ 16. Принципи найменшої дії

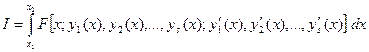 , (15.10)
, (15.10)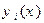 й їхніх похідних
й їхніх похідних  . Основна варіаційна задача в застосуванні до (15.10) складається в знаходженні такого набору функцій
. Основна варіаційна задача в застосуванні до (15.10) складається в знаходженні такого набору функцій 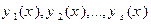 , які: 1) реалізують екстремум функціонала (15.10) і 2) задовольняють граничним умовам:
, які: 1) реалізують екстремум функціонала (15.10) і 2) задовольняють граничним умовам: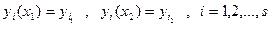 , (15.11)
, (15.11)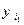 ,
, 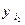 - задані величини.
- задані величини.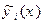 , близькі до
, близькі до 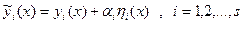 , (15.12)
, (15.12)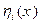 - довільні функції, що задовольняють граничним умовам:
- довільні функції, що задовольняють граничним умовам: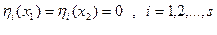 , (15.13)
, (15.13)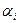 - малі чисельні параметри. Зводимо задачу до відшукання екстремуму функції:
- малі чисельні параметри. Зводимо задачу до відшукання екстремуму функції: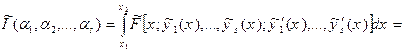
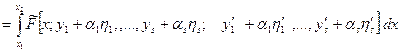 . (15.14)
. (15.14)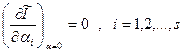 , (15.15)
, (15.15)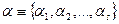 . Множачи кожне i- ту рівність (15.15) на
. Множачи кожне i- ту рівність (15.15) на 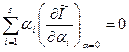 . (15.16)
. (15.16)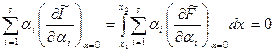 (15.17)
(15.17)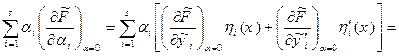
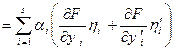 . (15.18)
. (15.18)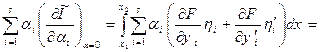
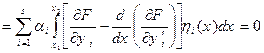 . (15.19)
. (15.19) , що реалізують екстремум функціонала (15.10), повинні задовольняти системі рівнянь Ейлера:
, що реалізують екстремум функціонала (15.10), повинні задовольняти системі рівнянь Ейлера: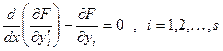 . (15.20)
. (15.20)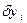 функцій
функцій 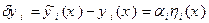 . (15.21)
. (15.21)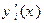 ; варіацію
; варіацію 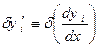 ми згідно (15.14) визначаємо формулою:
ми згідно (15.14) визначаємо формулою: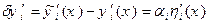 (15.22)
(15.22)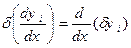 . (15.23)
. (15.23)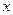 рівність (15.21)
рівність (15.21)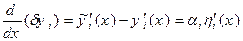 ,
,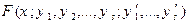 ; варіацією
; варіацією 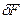 функції
функції 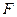 називається лінійна по
називається лінійна по  й
й 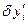 частина приросту
частина приросту 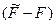 цієї функції, тобто:
цієї функції, тобто: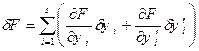 . (15.24)
. (15.24)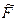 в ряд по
в ряд по  й обмежитися для
й обмежитися для 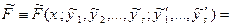
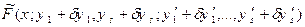 . Праві частини рівностей (15.24) і (15.18) рівні (з врахуванням (15.21) і (15.22)), тому формула:
. Праві частини рівностей (15.24) і (15.18) рівні (з врахуванням (15.21) і (15.22)), тому формула: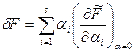 (15.25)
(15.25)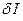 , обумовлену вираженням:
, обумовлену вираженням: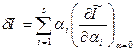 (15.26)
(15.26)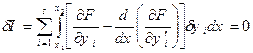 . (15.27)
. (15.27)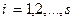 , що реалізують екстремум функціонала (15.10), повинні перетворювати в нуль варіацію функціонала
, що реалізують екстремум функціонала (15.10), повинні перетворювати в нуль варіацію функціонала 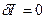 має місце тільки при виконанні рівнянь Ейлера (15.20).
має місце тільки при виконанні рівнянь Ейлера (15.20).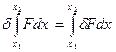 . (15.28)
. (15.28)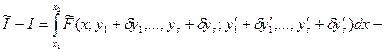
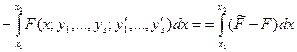 , (15.29)
, (15.29)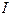 внаслідок варіації функцій
внаслідок варіації функцій 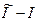 , що математично некоректно). Для одержання явного виразу для
, що математично некоректно). Для одержання явного виразу для 
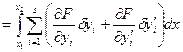 . (15.30)
. (15.30)


