Рівняння Гамільтона-Якобі.
Для формулювання принципу найменшої дії Гамільтона-Остроградського ми в §16 визначили дію S механічної системи як певний інтеграл:
залежний від вигляду конфігураційних траєкторій системи, що починаються й закінчуються у двох заданих конфігураціях Можлива, однак, і постановка таких фізичних задач, коли дійсні рухи системи можуть: 1) “ закінчуватись ” у різних конфігураціях 2) відбуваються з однієї конфігурації в іншу за різні проміжки часу
Використовуючи (17.3), (19.2) можна переписати у вигляді (див. також (17.6)):
звідки для повного диференціала
З іншого боку, формальний вираз для повного диференціала від функції
З порівнянням (19.4) і (19.5) знаходимо:
Якщо тепер у співвідношенні (19.6) узагальнені імпульси
якому повинна задовольняти функція дії
Поряд з методом Лагранжа й Гамільтона рівняння (19.8) становить основу ще одного методу інтегрування рівняння руху, що тут не викладається. Важливе значення рівняння Гамільтона-Якобі (19.8) полягає в тому, що воно допомагає: 1) розкрити аналогію між класичною механікою частки й хвильовим процесом (т.зв. оптико-механічну аналогію), що відіграє важливу роль при поясненні хвильових властивостей мікрочастинок у квантовій механіці; 2) установити граничний перехід від квантової механіки до механіки класичної (див. частина IV). Заключне зауваження. Аналітичні методи дослідження механічного руху, викладені в главі 3, розвинені на основі механічної картини світу, тобто на основі примітивних (із сучасної точки зору) уявлень про фізичну форму руху матерії, і тому, на перший погляд, не можуть бути використані за межами МКС. Однак, як ми вже неодноразово підкреслювали, ці методи при відповідному їхньому узагальненні з більшим успіхом застосовуються й у рамках інших ФКС – ЕМКС і КПКС. Ця обставина чітко підтверджує єдність фізичної реальності і є переконливою природно науковою ілюстрацією положення діалектичного матеріалізму про єдність матеріального світу. Ця ж обставина дає переконливу відповідь на питання, чому серйозне вивчення «древньої» науки – класичної механіки так необхідно для виховання сучасного фізика-дослідника.
|

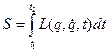 , (19.1)
, (19.1)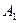 й
й 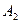 у задані моменти часу
у задані моменти часу 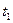 й
й 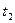 (див. мал. 16.1)).
(див. мал. 16.1)).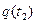 ,
,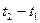 . Такими є задачі, пов'язані з розглядом безлічі різнихдійсних рухів системи, які відрізняються друг від друга різним вибором її початкового стану (точніше, різним вибором її узагальнених початкових швидкостей
. Такими є задачі, пов'язані з розглядом безлічі різнихдійсних рухів системи, які відрізняються друг від друга різним вибором її початкового стану (точніше, різним вибором її узагальнених початкових швидкостей 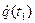 при однаковій початковій конфігурації
при однаковій початковій конфігурації 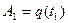 – див. мал. (16.1)). Так як при такій постановці задач всі досліджувані рухи системи є дійсними, то всі розглянуті при цьому конфігураційні траєкторії автоматично задовольняють рівнянням Лагранжа (13.18). Т. ч., у самому загальному випадку (враховуючому й викладену вище можливість постановки фізичних задач), поняття про дію механічної системи (19.1) варто узагальнити й розглядати дію
– див. мал. (16.1)). Так як при такій постановці задач всі досліджувані рухи системи є дійсними, то всі розглянуті при цьому конфігураційні траєкторії автоматично задовольняють рівнянням Лагранжа (13.18). Т. ч., у самому загальному випадку (враховуючому й викладену вище можливість постановки фізичних задач), поняття про дію механічної системи (19.1) варто узагальнити й розглядати дію 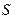 як явну функцію
як явну функцію 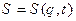 кінцевого моменту часу
кінцевого моменту часу 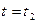 й кінцевої конфігурації системи
й кінцевої конфігурації системи 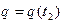 , тобто дія системи в загальному випадку можна визначитися невизначеним інтегралом:
, тобто дія системи в загальному випадку можна визначитися невизначеним інтегралом: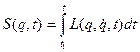 . (19.2)
. (19.2)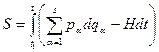 , (19.3)
, (19.3) одержуємо вираз:
одержуємо вираз: . (19.4)
. (19.4) має вигляд:
має вигляд: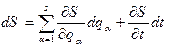 . (19.5)
. (19.5)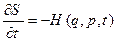 (19.6)
(19.6) ,
,  (19.7)
(19.7)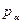 , що входять у функцію Гамільтона, замінити згідно (19.7) частковими похідними
, що входять у функцію Гамільтона, замінити згідно (19.7) частковими похідними 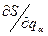 , то ми одержимо рівняння:
, то ми одержимо рівняння: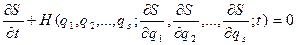 , (19.8)
, (19.8) механічної системи з узагальнено-потенційними активними силами й голономними ідеальними в'язями. Це рівняння в частинних похідних першого порядку називається рівнянням Гамільтона-Якобі. Воно є нелінійним рівнянням, тому що часткові похідні
механічної системи з узагальнено-потенційними активними силами й голономними ідеальними в'язями. Це рівняння в частинних похідних першого порядку називається рівнянням Гамільтона-Якобі. Воно є нелінійним рівнянням, тому що часткові похідні  , що рухається в потенціальному полі
, що рухається в потенціальному полі 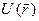 , функція Гамільтона має вигляд
, функція Гамільтона має вигляд 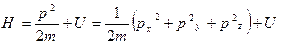 ; тому рівняння Гамільтона-Якобі (19.8) для такої системи записується у вигляді (якщо як узагальнені координати точки використати її декартові координати):
; тому рівняння Гамільтона-Якобі (19.8) для такої системи записується у вигляді (якщо як узагальнені координати точки використати її декартові координати):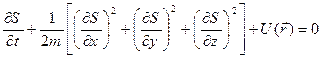 . (19.9)
. (19.9)


