Пропорциональное звено
Уравнение звена Передаточная функция Переходная функция Импульсная переходная функция представляет мгновенный бесконечно большой амплитудой импульс.
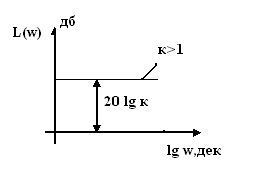
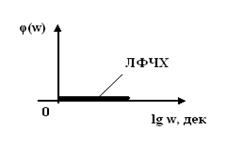
Площадь мгновенного импульса равняется коэффициенту передачи звено. Частотные характеристики КПФ звена W(jω)=к. АФЧХ звена в комплексной плоскости представляет точку на вещественной оси, удаленную от начало координат на расстояние к. Модуль КПФ А(ω)=к, т.е. амплитуда выходного колебания не зависят от частоты. Аргумент КПФ φ(ω)=0, т.е. выходные колебания совпадает по фазе с колебаниями на входе на всех частотах (сдвиг фаз отсутствует). Выражение ЛАЧХ звена имеет вид ЛАЧХ звена представляет прямую, параллельную оси частот (рис. 6.1) ЛФЧХ звена представляет прямую, совпадающей с положительной вещественной осью (φ(ω)=0).
Рисунок 9.1. ЛАЧХ и ЛФЧХ пропорционального звена
Идеальное апериодическое звено 1-го порядка. Уравнение звена Передаточная функция звена Переходная функция звена Переходная характеристика (рис. 6.2а) изменяется по экспоненциальному закону. Выходная величина звена достигает своего установившегося значения не сразу, а постепенно, через t=(3÷4)T. В этом проявляется инерционность звена. Поэтому это звено иногда называют инерционным. А) Рисунок 9.2 а) Переходная характеристика, б) импульсно переходная характеристика Импульсная переходная функция Частотные характеристики КПФ звена определяется выражением
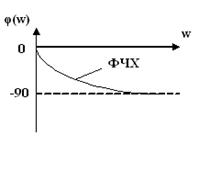
АФЧХ звена в комплексной плоскости представляется полуокружностью с диаметром, равной передаточному коэффициенту звено К. Центр окружности лежит в точке (К/2, 0). Модуль КПФ т.е с увеличением частоты амплитуда выходного сигнала убивает Рисунок 9.3 АЧХ и ФЧХ звена
Аргумент КПФ С увеличением частоты сдвиг фаз между входными и выходными колебаниями увеличивается, достигая в пределе к –90°. Выражения ЛАЧХ звена Для области низких (ω«1/T) и высоких (ω»1/T) частот выражения для L(ω) может быть упрощено
L (ω) = 20 lg к, при ω<<1/T L (ω) = 20 lg к – 20 lg ω*Т, при ω>>1/T
ЛАЧХ звена в области низких частот представляет прямую АС, параллельное оси частот (асимтота точкой ЛАЧХ в области низких частот) ЛАЧХ в области высоких частот представляет прямую СВ с наклоном – 20 дб/дек (асимтота точкой ЛАЧХ в области высоких частот). Пересечение асимтот происходит при частоте ω с =1/Т и называется частотой сопряжения (рис. 9.4 а). ЛФЧХ звена при увеличении частоты по абсолютной величине увеличивается и стремится к – 90°. (рис. 6.4 б) а) Рисунок 9.4 а)–ЛАЧХ и б) – ЛФЧХ звена 2. ПИД – регулятор. ПИД – регуляторам называется регулятор, у которого перемещение РО пропорционально отклонению регулируемой величины от задания, интегралу от этого отклонения и скорости его изменения, т.е.
где Передаточная функция ПИД – регулятора
Как видно из уравнения (13.7), регулирующее воздействие состоит из пропорциональной, интегральной и дифференциальной составляющих. Последняя из них тем больше, чем больше скорость изменения отклонения регулируемой величины, т.е. регулирующее воздействие вырабатывается как бы заранее, не дожидаясь наступления значительного отклонение регулируемой величины. Введение дифференциальной составляющей закон регулирования позволяет улучшить качество переходного процесса в АСР. Однако, настройка ПИД – регулятора, связанная с определением трёх параметров, сложна, при неправильной настройке качество регулирования может оказаться хуже, чем при использовании более простых регуляторов.
|

 , где x(t) – входная, y(t) – выходная величины, к – передаточный коэффициент.
, где x(t) – входная, y(t) – выходная величины, к – передаточный коэффициент.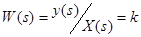
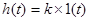 , т.е. при подаче на вход звена единичного скачка, выходная величина копирует изменение входной величины без запаздывания и искажения, но в другом масштабе. Поэтому пропорциональное звено называют еще безинерционным.
, т.е. при подаче на вход звена единичного скачка, выходная величина копирует изменение входной величины без запаздывания и искажения, но в другом масштабе. Поэтому пропорциональное звено называют еще безинерционным.
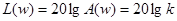
 , где Т – постоянная времени (характеризует инерционность звена).
, где Т – постоянная времени (характеризует инерционность звена).
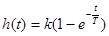
 б)
б) 
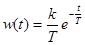 , т.е. убывает по экспоненциальному закону (рис. 6.2б)
, т.е. убывает по экспоненциальному закону (рис. 6.2б)
 ,
,
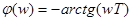 .
.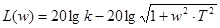 ;
; б)
б) 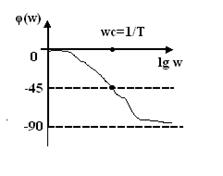
 (13.7)
(13.7) = 1/Тии
= 1/Тии  = Тд – параметры настройки ПИД–регулятора, Тд-время дифференцирования
= Тд – параметры настройки ПИД–регулятора, Тд-время дифференцирования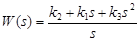 (13.8)
(13.8)


