Алгебраический критерий устойчивости Гурвица.Алгебраический критерий устойчивости Гурвица применяется для замкнутых систем. Однако, как правило, известна W(s) разомкнутой САУ. В этом случая надо ”мысленно” замкнуть систему единичной обратной отрицательной связью (ООС), найти передаточную функцию замкнутой системы по формуле Wз(s)= и записать характеристическое уравнение системы Q2(s)=0,
т.е. a0sn+ a1sn-1+...+ an-1s+ an=0.
Формулировка критерия устойчивости Гурвица: для устойчивости замкнутой САУ необходимо и достаточно, чтобы при a0>0 все миноры, расположенные по главной диагонали определителя Гурвица, были строго положительны. Определитель Гурвица строится по коэффициентам характеристического уравнения следующим образом: D(n*n)= где n-порядок системы. Из формулировки критерия устойчивости Гурвица следует, что при а0>0 для устойчивости системы необходимо и достаточно, чтобы D1=a1>0 D2= D3= Различают три типа границы устойчивости системы из условия Dn=anDn-1=0
Это следующие границы: 4) первый тип границы устойчивости, который называется апериодической границей устойчивости an=0; 5) второй тип границы устойчивости, который называется колебательной границей устойчивости Dn-1=0; 6) третий тип границы устойчивости называется бесконечной a0=0, когда один из корней характеристического уравнения равен бесконечности, т.е. sj=¥ Следует отметить, что наиболее опасной является нахождение системы на колебательной границы устойчивости.
|
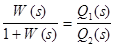
>0
>0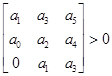
и т.д.
