Идеальное апериодическое звено 1-го порядка.
Уравнение звена Передаточная функция звена Переходная функция звена Переходная характеристика (рис. 6.2а) изменяется по экспоненциальному закону. Выходная величина звена достигает своего установившегося значения не сразу, а постепенно, через t=(3÷4)T. В этом проявляется инерционность звена. Поэтому это звено иногда называют инерционным. А) Рисунок 9.2 а) Переходная характеристика, б) импульсно переходная характеристика Импульсная переходная функция Частотные характеристики КПФ звена определяется выражением
АФЧХ звена в комплексной плоскости представляется полуокружностью с диаметром, равной передаточному коэффициенту звено К. Центр окружности лежит в точке (К/2, 0). Модуль КПФ т.е с увеличением частоты амплитуда выходного сигнала убивает Рисунок 9.3 АЧХ и ФЧХ звена
Аргумент КПФ С увеличением частоты сдвиг фаз между входными и выходными колебаниями увеличивается, достигая в пределе к –90°. Выражения ЛАЧХ звена Для области низких (ω«1/T) и высоких (ω»1/T) частот выражения для L(ω) может быть упрощено
L (ω) = 20 lg к, при ω<<1/T L (ω) = 20 lg к – 20 lg ω*Т, при ω>>1/T
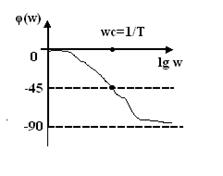
ЛАЧХ звена в области низких частот представляет прямую АС, параллельное оси частот (асимтота точкой ЛАЧХ в области низких частот) ЛАЧХ в области высоких частот представляет прямую СВ с наклоном – 20 дб/дек (асимтота точкой ЛАЧХ в области высоких частот). Пересечение асимтот происходит при частоте ω с =1/Т и называется частотой сопряжения (рис. 9.4 а). ЛФЧХ звена при увеличении частоты по абсолютной величине увеличивается и стремится к – 90°. (рис. 6.4 б) а) Рисунок 9.4 а)–ЛАЧХ и б) – ЛФЧХ звена
|

 , где Т – постоянная времени (характеризует инерционность звена).
, где Т – постоянная времени (характеризует инерционность звена).
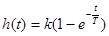
 б)
б) 
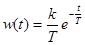 , т.е. убывает по экспоненциальному закону (рис. 6.2б)
, т.е. убывает по экспоненциальному закону (рис. 6.2б)
 ,
,
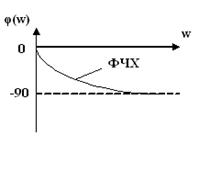
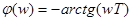 .
.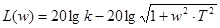 ;
; б)
б)