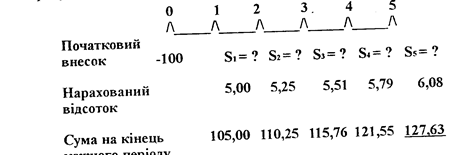Концепція тимчасової вартості грошей
Стара приказка про те, що краще синиця в руках, аніж журавель у небі, безпосередньо стосується фінансів. Це означає, що сьогодні гроші мають більшу вартість, ніж завтра: з плином часу вартість грошей змінюється. Інвестори, звісна річ, віддають перевагу грошам, які с сьогодні, а не тим, що будуть завтра, бо вони дають їм змогу з тих грошей зробити ще гроші. Це, звичайно, основна мета фінансового менеджера. Окрім тої о, що гроші сьогодні мають більшу вартість, ніж гроші в майбутньому, слід ще пам'ятати, що вони з часом частково втрачають свою вартість. Основні причини втрати вартості ірошей: • інфляція; • ризик; • схильність до ліквідності. Одним з найважливіших інструментів проведення аналізу тимчасової вартості грошей є часова лінія. Графічний вираз тим- ринок фінансових послуг: теорія і практика часового розподілу потоку готівки відтворює діаграма А: Діаграма А
Кожний штрих на лінії відмічає кінець одного періоду і, в той же час, початок наступного. Іншими словами, штрих І на часовій лінії відмічає кінець року 1 і початок року 2. Діаграма В
У випадку, показаному на діаграмі В, відсоткова ставка для усіх трьох періодів становить 5 відсотків. Під час 0 трапився одноразовий відплив потоку готівки, під час 3 очікується невідомий приплив готівки. Відплив - це витрати, виплати, депозити готівкою. Приплив - прийняття готівки. Діаграма С
На діаграмі С відсоткова ставка у перший період становить 5 відсотків, але протягом другого періоду вона виросте до 10 відсотків. Якщо відсоткова ставка постійна протягом усіх періодів, ми вказуємо її тільки для першого періоду, якщо ж вона змінюється, то її вказують для кожного періоду окремо. Часові лінії дуже важливі для початкового розуміння концепцій тимчасової вартості грошей, але навіть досвідчені спеціалісти користуються нею для проведення складного аналізу проблем. Долар, який ми маємо наданий момент, коштує дорожче, ніж долар, отриманий у майбутньому. Це відбувається тому, що якщо ви маєте його зараз, то можете його вкласти у будь-яку справу і одержати відсоток, що однаково дасть суму, більшу ніж долар, який ви отримаєте у майбутньому. Майбутня вартість - сума, до якої виросте грошовий потік чи серія грошових потоків протягом даного періоду часу при даній процентній ставці. Цей процес продовжується, і внаслідок того, що кожного разу початкова сума вище попередньої, річний відсоток зростає. Ходаківська В. II., Веляєв В. В Процес переходу від теперішньої вартості (Р) до майбутньої вартості (S) називається компаундируванням. Приклад. Припустимо, що ви поклали у банк 100 доларів під 5 відсотків річних. Яку суму ви будете мати наприкінці першого року? S у такому випадку необхідно розраховувати наступним чином: S = Si = Р + Рі = Р (1 + і) = S 100 (1 + 0,05) = $ 100 (1,05) = S 105. S = Р (1 + пі). Відповідно до цього рівняння майбутня вартість після закінчення одного року дорівнює початковій ставці, помноженій на 1,0 плюс відсоткова ставка. Яким же буде результат, якщо ви залишите свої 100 доларів на банківському рахунку на 5 років? Для того, щоб краще не зоозуміти, слід накреслити часову лінію:
Відмітьте, що вартість наприкінці 2 року, $ 110/25,дорівнює S;°= S, (1 + і) = Р (1 + і) (1 + і) = Р (1 + і);= S 100 (1,05), = S 110,25. Кінцевий результат третього року внеску: S,= Si (1 + і) = P(l + і) (1 + і) (1 + і) = Р(1 + і)і= S 100 (1,05> = S 115,76. 1, нарешті: S.= S< (1+ і) = Р (1 + і) (1 + і) (1 + і) (1 + і) (1 + і) = Р (1 + і). = S 100 (1,05)з -- S 127.63. Взагалі, майбутня вартість початкової суми на кінець п-ої кількості років може бути визначена за допомогою рівняння: S = Р (1 + і)п. Поняття поточної вартості. Припустимо, що у вас з'явились вільні гроші, 100 доларів США, і ви маєте можливість придбати цінні папери з низьким відсотком ризику, за якими через 5 років отримаєте 127,63 долара. Ваш місцевий банк на даний час пропонує 5 відсотків річних за внеском на 5 років, і ви вважаєте, що ці цінні папери такі ж надійні, як і ощадні сертифікати. Ставка 5 відсотків може бути визначена як ставка "ціни шансу" ринок фінансових послуг: теорія і практика або ставка прибутку, який ви могли б одержати за іншим внеском з таким же ступенем ризику. Отже, запи тання: яку суму ви були б згодні заплатити за дані цінні папери? З прикладу майбутньої вартості ми зрозуміли, що первісна сума в 100 доларів США, покладена в банк під 5% річних, після закінчення 5 років матиме вартість у 127,63 долара США. 100 доларів США у даному випадку визначаються як поточна вартість (Р) суми в 127,63 долара США у майбутньому, через 5 років. Поточна вартість потоку готівки, очікувана через п-у кількість років у майбутньому - це сума, яка (якщо є в наявності на сьогодні), виросте до рівня суми, що дорівнює майбутній. Через те, що S 100 при 5-процентній річній ставці виросте за 5 років до суми $ 127,63, то $ 100 е поточною вартістю суми S 127,63 при 5-процентній ставці та за 5 років. Дія визначення поточної вартості називається дисконтуванням і є прямою протилежністю компаундируванню. Поточна вартість 1 долара США (або будь-якої іншої суми), яку вкладник очікує отримати у майбутньому, графічно зменшуватиметься із плином часу відповідно до того, як збільшуються показники років. При відносно високій відсотковій ставці сума, яку вкладник розраховує одержати в майбутньому, коштує в поточний момент небагато. Навіть якщо відсоткова ставка низька, поточна вартість суми, що повинна виплатитись через досить довгий час, досить мала. Наприклад, при 20-відсотковій дисконтній ставці 1млн. доларів через 100 років буде мати вартість усього 1 цента сьогоднішнього дня (проте 1 цент при 20-відсотковій ставці за 100 років виросте до 1млн. доларів). Розрахунки тимчасової вартості грошей майже завжди виконуються за допомогою рівнянь із чотирма невідомими. Тому, якщо вам відомо три з них, ви (або ваш калькулятор) можете легко розрахувати четверту. Так, якщо вам відомі суми окремих потоків готівки і Р (або S) всього потоку готівки, ви можете розрахувати відсоткову ставку. На практиці значно частіше, ніж раз на рік, проводяться виплати та нараховуються відсотки, тому кількість років необхідно замінити в таких випадках на кількість періодів. Поняттями, розглянутими вище, ми будемо користуватись при обміркуванні проблем прийняття фінансових рішень у різних фінансових ситуаціях з використанням рівнянь із чотирма невідомими.
|