Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай. Нулевая гипотеза H₀:D(X) — D(Y). Конкурирующая гипотеза H_xiD ( X) > D(Y).

В этом случае строят одностороннюю, а именно пра­востороннюю, критическую область, исходя из требова­ния, чтобы вероятность попадания критерия F в эту область в предположении справедливости нулевой гипо­тезы была равна принятому уровню значимости:

Критическую точку F_KP (а; k_lt k_t) находят по таблице критических точек распределения Фишера—Снедекора (см. приложение 7), и тогда правосторонняя критическая область определяется неравенством F > F_KP, а область принятия нулевой гипотезы — неравенством F < F_Kp.

Правило 1. Для того чтобы при заданном уровне зна­чимости проверить нулевую гипотезу H₀:D (X) = D (Y) о равенстве генеральных дисперсий нормальных совокуп­ностей при конкурирующей гипотезе tf₁:D(X)> D(Y), надо вычислить отношение большей исправленной диспер­сии к меньшей, т. е.

Пример 1. По двум независимым выборкам объемов я*=12 и п_г= 15, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии sx = 11,41 и s^, = 6,52. При уровне значимости 0,05 проверить нулевую гипотезу H_C:D(X) = D(Y ) о равенстве генеральных дисперсий при конкури­рующей гипотезе H₁:D(X) > D (Y).

Решение. Найдем отношение большей исправленной дисперсии к меньшей:

^набл — 11,41/6,52 = 1,75.

Конкурирующая гипотеза Имеет вид D (X) > D (Y), поэтому крити­ческая область — правосторонняя.

По таблице приложения 7, по уровню значимости а = 0,05 и числам степеней свободы fe₁=l2 — 1 = 11 и fr₂ = 15—1 = 14 находим критическую точку F„ j, (0,05; 11, 14) = 2,56.

Так как Г_набл < Ркр — нет оснований отвергнуть нулевую гипо­тезу о равенстве генеральных дисперсий.

Второй случай. Нулевая гипотеза H₀:D (Х) = £>(К). Конкурирующая гипотеза Н^'.D (X) фD (Y).

В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попа­

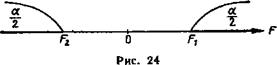
дания критерия в эту область в предположении спра­ведливости нулевой гипотезы была равна принятому уровню значимости а.

Как выбрать границы критической области? Оказы­вается, что наибольшая мощность (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда вероят­ность попадания критерия в каждый из двух интервалов критической области равна а/2.

Таким образом, если обозначить черег F_t левую границу критической области и через Р_г — правую, то должны иметь место соотношения (рис. 24):

а также область принятия нулевой гипотезы: F_x < F < F_t. Как практически отыскать критические точки?

Правую критическую точку F_t = F_KX>(а/2; k_lt k₃) нахо­дят непосредственно по таблице критических точек рас­пределения Фишера — Снедекора по уровню значимости а/2 и степеням свободы k_x и k₃.

Однако левых критических точек эта таблица не со­держит и поэтому найти F_x непосредственно по таблице невозможно. Существует способ, позволяющий преодолеть это затруднение. Однако мы не будем его описывать, поскольку можно левую критическую точку и не отыски­вать. Ограничимся изложением того, как обеспечить по­падание критерия F в двустороннюю критическую область с вероятностью, равной принятому уровню значимости а.

Оказывается, достаточно найти правую критическую точку р₉ при уровне значимости, вдвое меньшем заданного. Тогда не только вероятность попадания критерия в «пра­вую часть» критической области (т. е. правее F_s) равна а/2, но и вероятность попадания этого критерия в «левую часть» критической области (т. е. левее F_t) также равна а/2. Так как эти события несовместны, то вероятность попадания рассматриваемого критерия во всю двусторон­нюю критическую область будет равна а/2 + а/2 = а.

Таким образом, в случае конкурирующей гипотезы H₁:D(X)¥^zD(Y) достаточно найти критическую точку F, = F_KP (а/2; k_x, k_t).

Правило 2. Для того чтобы при заданном уровне зна­чимости а проверить нулевую гипотезу о равенстве гене­ральных дисперсий нормально распределенных совокуп­ностей при конкурирующей гипотезе H_X-.D (X) Фй (Y), надо вычислить отношение большей исправленной дис­персии к меньшей, т. е. F_Ha6x = sl/sl_l и по таблице кри­тических точек распределения Фишера—Снедекора по уровню значимости а/2 (вдвое меньшем заданного) и чис­лам степеней свободы к_г и k_t (k_t —число степеней свободы большей дисперсии) найти критическую точку F_Kp(а/2;

Если F„_a^_a <С F _KV—^нет оснований отвергнуть нулевую гипотезу. Если F_Haв_л > F _KV—нулевую гипотезу отвергают.

Пример 2. По двум независимым выборкам, объемы которых соответственно равны ni=10 и л_г=18, извлеченным из нормальных генеральных совокупностей X и У, найдены исправленные выбороч­ные дисперсии = 1,23 и s|, = 0,41. При уровне значимости а = 0,1

проверить нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей гипотезе H\.D (X) ф D (Y).

Решение. Найдем отношение большей исправленной дисперсии к меньшей:

^набл ⁼ 1 >23/0,41 = 3.

По условию, конкурирующая гипотеза имеет вид D(X)^D(Y), поэтому критическая область—двусторонняя.

По таблице, по уровню значимости, вдвое меньшем заданного, т. е. при а/2 = 0,1/2 = 0,05, и числам степеней свободы Л₁=10—1=9, fe₂=18—1 = 17 находим критическую точку F_KV (0,05, 9, 17) = 2,50.