Стаціонарний потенціал Гольдмана-Ходжкіна-Катца
Розбіжності між експериментальними значеннями потенціалу спокою на мембрані і розрахованими за рівнянням Нернста для рівноважного потенціалу (мал. 6.32) пов’язані, насамперед, з тим, що мембрана проникна не лише для іонів К+, але й для інших іонів. Наявність сумарного потоку для цих іонів приводить до виникнення мембранної різниці потенціалів, яка починає гальмувати транспорт іонів, внаслідок чого сумарний електричний струм іонів ( Саме цим стаціонарний потенціал відрізняється від рівноважного потенціалу Нернста, умовою виникнення якого є рівність нулеві потоку лише одного певного сорту іонів. У теорії стаціонарного потенціалу, розвиненої Д. Гольдманом, А. Ходжкіним і Б. Катцем, враховувалися внески в сумарний потік лише одновалентних іонів натрію, калію і хлору. Розраховуючи мембранний потенціал, що виникає за цих умов, автори виходили з таких положень: 1) здійснюється умова стаціонарності
2) у мембрані спостерігається сталість градієнту електричного потенціалу
3) потік кожного сорту іонів підпорядковується рівнянню Нернста-Планка
де i – індекс сорту іонів, i = Na+, К+, Сl–. Інтегрування рівнянь (6.57) з урахуванням умови стаціонарності ФNa + ФK – ФCl = 0 дозволяє одержати вираз для мембранного потенціалу (див. деталі нижче)
де Р Na, Р K, P Cl – проникності мембрани для відповідних іонів. Рівняння Гольдмана значно краще узгоджується з експериментальними даними, ніж рівняння Нернста (мал. 6.32). Легко переконатись, що рівняння Нернста є частинним випадком рівняння Гольдмана. Дійсно, в спокої у гігантському аксоні кальмара Р Na: Р K: P Cl= 1:0.04:0.045, тобто Р K >> P Cl, Р K >> P Na. У цьому випадку:
Вираз для стаціонарного мембранного потенціалу можна одержати, використовуючи безрозмірний мембранний потенціал
де L – товщина мембрани, а саме:
звідки
або
Проінтегруємо рівняння (6.59) по всій товщині мембрани
звідки
або
Оскільки сім = Kсі, сем = Kсе (див. мал. 6.24), то рівняння (6.60) набуває вигляду:
або
де P = DK/L – проникність мембрани. Одержимо вираз для стаціонарного мембранного потенціалу, що виникає при наявності потоку іонів Na+ y клітину, потоку іонів К+ зовні і потоку іонів Сl– у клітину при умові, що загальний потік
Використовуючи (6.61), з умови (6.62) отримаємо:
звідки
або
З урахуванням того, що
Враховуючи внесок потоку іонів Сl–, одержимо з (6.64) вираз (6.58):
|

 ),а отже і сумарний потік іонів (
),а отже і сумарний потік іонів (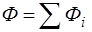 )припиняється. При цьому на мембрані встановлюється різниця потенціалів, спричинена не умовою рівноваги (
)припиняється. При цьому на мембрані встановлюється різниця потенціалів, спричинена не умовою рівноваги ( ),а умовою стаціонарності, яка означає, що повний потік, обумовлений потоками всіх іонів, дорівнює нулю (
),а умовою стаціонарності, яка означає, що повний потік, обумовлений потоками всіх іонів, дорівнює нулю ( ), при цьому кожний з потоків у загальному випадку відмінний від нуля (
), при цьому кожний з потоків у загальному випадку відмінний від нуля (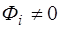 ).
). ;
;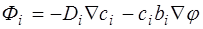 , (6.57)
, (6.57) (6.58)
(6.58) для іонів K+.
для іонів K+. . Для цього дещо перетворимо рівняння Нернста-Планка, використавши умову сталості градієнта потенціала в мембрані
. Для цього дещо перетворимо рівняння Нернста-Планка, використавши умову сталості градієнта потенціала в мембрані ,
, ,
, ,
, . (6.59)
. (6.59) ,
,  ,
, ,
, . (6.60)
. (6.60) ,
,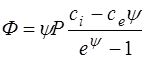 , (6.61)
, (6.61) .
.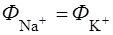 . (6.62)
. (6.62)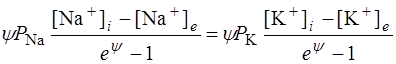 ,
, ,
,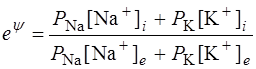 . (6.63)
. (6.63)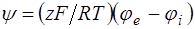 , з (6.63) маємо:
, з (6.63) маємо: . (6.64)
. (6.64) .
.


