Строкові депозити в Національному банку України

Дата добавления: 2014-12-06; просмотров: 604

Определение. Элементарным исходом (или элементарным событием) называют любой простейший (т.е. неделимый в рамках данного опыта) исход опыта. Множество всех элементарных исходов будем называть пространством элементарных исходов.

Другими словами, множество исходов опыта образует пространство элементарных исходов, если выполнены следующие требования:

- в результате опыта один из исходов обязательно происходит;

- появление одного из исходов опыта исключает появление остальных;

- в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.

Ω − пространство элементарных исходов, ω − сами элементарные исходы

Пример. Подбрасывание монеты ("идеальная монета"). Два исхода: выпадение герба (ω₁ = ω_Г) и выпадение цифры (ω₂ = ω_Ц).

При двукратном подбрасывании 4 исхода

Определение. Любой набор элементарных исходов, или, иными словами, произвольное подмножество пространства элементарных исходов, называют событием.

Элементарные исходы, которые являются элементами рассматриваемого подмножества (события), называют элементарными исходами, благоприятствующими данному событию, или образующими это событие.

События обозначают прописными латинскими буквами, снабжая их при необходимости индексами (А, B_i, C₃).

Часто используется следующая терминология: говорят, что событие А произошло (или наступило), если в результате опыта появился какой-либо из элементарных исходов .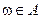

Определение. Событие, состоящее из всех элементарных исходов, т.е. событие, которое обязательно происходит в данном опыте, называют достоверным событием.

Определение. Событие, не содержащее ни одного элементарного исхода, т.е. событие, которое никогда не происходит в данном опыте, называют невозможным событием.

Пример. При бросании игральной кости достоверное событие можно описать, например, как выпадение хотя бы одного очка, а невозможное − как выпадение 7 очков.

Часто бывает полезно наглядно представить события в виде диаграммы Эйлера−Венна.

Определение. Пересечением (произведением) двух событий А и В называют событие С, происходящее тогда и только тогда, когда одновременно происходят оба события А и В, т.е. событие, состоящее из тех и только тех элементарных исходов, которые принадлежат и событию А, и событию В.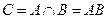

Определение. События А и В называют несовместными, или непересекающимися, если их пересечение является невозможным событием, т.е. если .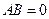

Определение. Объединением (суммой) двух событий А и В называют событие С, происходящее тогда и только тогда, когда происходит хотя бы одно из событий А или B, т.е. событие С, состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из подмножеств А или В.

Если события А и В несовместны, наряду со знаком 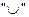для их объединения употребляют знак "+".

Аналогично определяют понятия произведения и суммы событий для любого конечного числа событий и даже для бесконечных последовательностей событий.

Определение. Разностью двух событий А и В называют событие С, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В, т.е. событие С, состоящее из тех элементарных исходов, которые принадлежат А, но не принадлежат В.

Определение. Дополнением события А (обычно обозначают 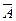) называют событие, происходящее тогда и только тогда, когда не происходит событие А. Другими словами, событие 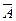называют также событием, противоположным событию А.

Определение. Событие А включено в событие В, если появление события А обязательно влечет за собой наступление события В, или каждый элементарный исход ω, принадлежащий А, обязательно принадлежит и событию В.