
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Боргові цінні папери, емітовані Національним банком України,у портфелібанку на інвестиції
Дата добавления: 2014-12-06; просмотров: 803
|
|
Вероятность события A, вычисленную в предположении, что событие B произошло, принято называть условной вероятностью и обозначать P(A|B).
Классическая схема. Пусть событиям A и B благоприятствуют NA и NB элементарных исходов соответственно. Посмотрим, что дает нам имеющаяся информация о событии B. Поскольку событие B произошло, то достоверно известно, что в результате опыта появился один из NB элементарных исходов, составляющих событие В. Значит, теперь уже при определении степени возможности события A необходимо выбирать только из NB возможных исходов, причем событию A благоприятствуют NAB исходов, при которых происходят и событие А, и событие B, или, другими словами, происходит событие AB. При этом по-прежнему будем считать все NB входящих в событие B исходов равновероятными. Поэтому условную вероятность P(A|B) события A при условии события B в рамках классической схемы вероятности естественно определить как отношение числа NAB исходов, благоприятствующих совместному осуществлению событий A и B, к числу NB исходов, благоприятствующих событию В, т.е.

Статистический подход. Пусть n – общее число экспериментов; nA – число экспериментов, в которых наблюдалось событие A; nB – число экспериментов, в которых наблюдалось событие B, nAB – число экспериментов, в которых наблюдалось событие AB. Условной частотой события A при условии, что B произошло естественно назвать частоту события A, но только не среди всех повторений опыта n, а лишь среди тех, в которых наблюдалось событие В, т.е.

Определение. Условной вероятностью события A при условии (наступлении) события B называют отношение вероятности пересечения событий A и B к вероятности события B:

При этом предполагают, что  .
.
В связи с появлением термина "условная вероятность" будем вероятность события называть также безусловной вероятностью события.
Теорема. Условная вероятность P(A|B) обладает всеми свойствами безусловной вероятности P(A).
Замечание. Условная вероятность представляет собой безусловную вероятность, заданную на новом пространстве Ω1 элементарных исходов, совпадающем с событием B.
Геометрическая интерпретация условной вероятности. При практическом вычислении условной вероятности события A при условии, что событие B произошло, часто удобно трактовать условную вероятность как безусловную, но заданную не на исходном пространстве Ω элементарных исходов, а на новом пространстве Ω1 = B элементарных исходов.
Теорема умножения вероятностей (формула для вероятности произведения нескольких зависимых событий). Если A = A1A2...An (т.е. А − пересечение событий A1, A2,..., An) и P(А)> 0, то справедливо равенство P(A)= P(A1)P(A2|A1)P(A3|A1A2)...P(An|A1A2...An − 1), называемое формулой умножения вероятностей.
Доказательство. Поскольку 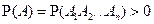 , а , а
 то и
то и  . Учитывая это неравенство, согласно определению условной вероятности, имеем . Учитывая это неравенство, согласно определению условной вероятности, имеем
 Умножая обе части этого равенства на
Умножая обе части этого равенства на  получаем получаем
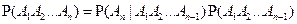 Аналогично находим
Аналогично находим
 .
Тогда .
Тогда
 Продолжая эту процедуру, получаем формулу умножения вероятностей.
Продолжая эту процедуру, получаем формулу умножения вероятностей.
|
Определение. События A и B, имеющие ненулевую вероятность, называют независимыми, если условная вероятность A при условии B совпадает с безусловной вероятностью A или если условная вероятность B при условии A совпадает с безусловной вероятностью B. В противном случае события A и B называют зависимыми.
Теорема. События A и B, имеющие ненулевую вероятность, являются независимыми тогда и только тогда, когда

Теорема. Если события A и B независимые, то независимыми также являются пары событий  и B, A и и B, A и  , ,  и и  , если вероятности соответствующих событий ненулевые. , если вероятности соответствующих событий ненулевые.
|
Определение. События А1, A2, ..., Аn называют независимыми в совокупности, если вероятность пересечения любых двух различных событий равна произведению вероятностей этих событий; вероятность пересечения любых трех событий равна произведению их вероятностей; ...; вероятность пересечения всех событий равна произведению их вероятностей.
Формула для вероятности произведения нескольких независимых событий). Если A = A1A2...An (т.е. А − пересечение событий A1, A2,..., An), P(А)> 0 и события А1, A2, ..., Аn независимы в совокупности, то справедливо равенство P(A)= P(A1)P(A2)P(A3)...P(An).
Теорема. Если события А1, A2, ..., Аn независимы в совокупности, то и события  независимы в совокупности.
Замечание. (о связи между совместными и зависимыми событиями). Между понятиями „несовместные" и „независимые" события имеется следующая связь:
1) если A и B − несовместные события (и независимы в совокупности.
Замечание. (о связи между совместными и зависимыми событиями). Между понятиями „несовместные" и „независимые" события имеется следующая связь:
1) если A и B − несовместные события (и  , и , и  ), то они обязательно зависимые (убедитесь самостоятельно);
2) если A и B − совместные события, то они могут быть и зависимыми, и независимыми;
3) если A и B − зависимые события, то они могут быть и совместными, и несовместными.
Следует помнить, что при использовании теоремы сложения вероятностей нужно проверять несовместность событий, а при использовании теоремы умножения − независимость событий. ), то они обязательно зависимые (убедитесь самостоятельно);
2) если A и B − совместные события, то они могут быть и зависимыми, и независимыми;
3) если A и B − зависимые события, то они могут быть и совместными, и несовместными.
Следует помнить, что при использовании теоремы сложения вероятностей нужно проверять несовместность событий, а при использовании теоремы умножения − независимость событий.
|
Формула для вероятности суммы нескольких совместных независимых событий.В прошлой лекции была получена формула:


В случае независимых, но совместных событий она примет вид


| <== предыдущая лекция | | | следующая лекция ==> |
| Боргові цінні папери, що рефінансуються Національним банком України, у портфелі банку на інвестиції | | | Резервипід знецінення боргових цінних паперів, щорефінансу-ються Національним банком України |