
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Резервипід знецінення боргових цінних паперів, щорефінансу-ються Національним банком України
Дата добавления: 2014-12-06; просмотров: 763
|
|
Предположим, что в результате опыта может произойти одно из n событий Н1, H2, ..., Нn, которые удовлетворяют следующим двум условиям:
1) они являются попарно несовместными, т.е. 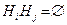 при i ≠ j.
при i ≠ j.
2) хотя бы одно из них обязательно должно произойти в результате опыта, другими словами, их объединение есть достоверное событие.
Определение. События Н1, H2, ..., Нn удовлетворяющие условиям 1 и 2, называют гипотезами.
Заметим, что если события удовлетворяют второму из двух указанных требований, то их совокупность называют полной группой событий. Таким образом, гипотезы – это попарно несовместные события, образующие полную группу событий.
Пусть также имеется некоторое событие А и известны вероятности гипотез P(Н1), ..., Р(Нn), которые предполагаются ненулевыми, и условные вероятности P(А|Н1), ..., P(A|Hn) события A при выполнении этих гипотез.
Теорема. Пусть для некоторого события A и гипотез Н1, H2, ..., Нn известны P(Н1), ..., P(Нn), которые положительны, и P(А|Н1), ..., P(A|Нn). Тогда безусловную вероятность определяют по формуле
P(A) = P(H1) P(А|Н1) +... + P(Нn) P(A|Нn)
которую называют формулой полной вероятности.
Доказательство. Представим событие А в виде
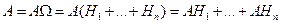 С учетом того, что события
С учетом того, что события 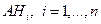 , несовместны, имеем , несовместны, имеем
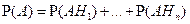 В соответствии с формулой умножения вероятностей получаем
В соответствии с формулой умножения вероятностей получаем
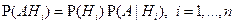
|
Теорема.Пусть длянекоторого события A,P(A)> 0, и гипотез H1, ..., Hn известны P(H1), ..., P(Hn) (P(Hi) > 0, i = 1, ..., n) и P(A|H1),..., P(A|Hn). Тогда условная вероятность P(Hi|A), i = 1, ..., n, гипотезы Hi при условии события A определяется формулой Байеса
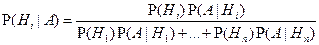
| <== предыдущая лекция | | | следующая лекция ==> |
| Боргові цінні папери, емітовані Національним банком України,у портфелібанку на інвестиції | | | Строкові депозити, які розміщені в інших банках |