
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Боргові цінні папери, що рефінансуються Національним банком України, у портфелі банку на продаж
Дата добавления: 2014-12-06; просмотров: 738
|
|
Геометрическое определение вероятности обобщает классическое на случай бесконечного множества элементарных исходов Ωтогда, когда Ωпредставляет собой подмножество пространства R (числовой прямой), R2 (плоскости), Rn (n-мерного евклидова пространства).
В пространстве R в качестве подмножеств будем рассматривать лишь промежутки или их объединения, т.е. подмножества, которые имеют длину. В пространстве R2 − те подмножества, которые имеют площадь, и т.д.
Под мерой  подмножества А будем понимать его длину, площадь или объем (обобщенный объем) в зависимости от того, какому пространству принадлежит Ω: в R, в R2 или в R3 (Rn) Будем также считать, что пространство элементарных исходов Ω имеет конечную меру, а вероятность попадания „случайно брошенной" точки в любое подмножество Ω пропорциональна мере этого подмножества и не зависит от его расположения и формы. В этом случае говорят, что рассматривается „геометрическая схема" или „точку наудачу бросают в область Ω".
подмножества А будем понимать его длину, площадь или объем (обобщенный объем) в зависимости от того, какому пространству принадлежит Ω: в R, в R2 или в R3 (Rn) Будем также считать, что пространство элементарных исходов Ω имеет конечную меру, а вероятность попадания „случайно брошенной" точки в любое подмножество Ω пропорциональна мере этого подмножества и не зависит от его расположения и формы. В этом случае говорят, что рассматривается „геометрическая схема" или „точку наудачу бросают в область Ω".
Определение. Вероятностью события А называют число P(A), равное отношению меры множества А к мере множества Ω:
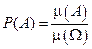
где  − мера множества А.
− мера множества А.
Данное определение вероятности события принято называть геометрическим определением вероятности. Заметим, что в литературе вероятность события А, определенную выше, на основе геометрической схемы, часто называют геометрической вероятностью. Геометрическая вероятность, очевидно, сохраняет отмеченные ранее свойства вероятности P(А) в условиях классической схемы.
| Статистическое определение вероятности.Вероятностью событияА называют (эмпирический) предел Р(A),к которому стремится частота rA события А при неограниченном увеличении числа n опытов. |
| <== предыдущая лекция | | | следующая лекция ==> |
| Строкові депозити Національногобанку України | | | Боргові цінні папери, що рефінансуються Національним банком України, у портфелі банку на інвестиції |