Довгострокові кредити, які отримані від Національного банку України

Дата добавления: 2014-12-06; просмотров: 778

Пусть каждому событию А (т.е. подмножеству А пространства элементарных исходов Ω, принадлежащему σ-алгебре B) поставлено в соответствие число P(A). Числовую функцию P (заданную на σ-алгебре B) называют вероятностью (или вероятностной мерой), если она удовлетворяет следующим аксиомам:

Аксиома 1 (аксиома неотрицательности): Р(A) ≥ 0;

Аксиома 2 (аксиома нормированности): Р(Ω) = 1;

Аксиома 3 (расширенная аксиома сложения):для любых попарно несовместных событий A₁,..., A_n,... справедливо равенство

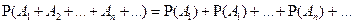
Значение P(A) называют вероятностью события А.

Теорема. Вероятность удовлетворяет следующим свойствам.

1. Вероятность противоположного события .

2. Вероятность невозможного события .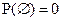

3. Если ,то („большему" событию соответствует большая вероятность).

4. Вероятность заключена между 0 и 1: 0 ≤ P(А) ≤ 1.

5. Вероятность объединения двух событий

.

6. Вероятность объединения любого конечного числа событий

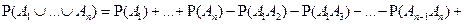
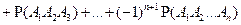
Доказательство. Поскольку , то, согласно расширенной аксиоме сложения, , откуда с учетом аксиомы нормированности получаем утверждение 1. Утверждение 2 вытекает из равенства и расширенной аксиомы сложения. Пусть . Тогда B = A + (B\A). В соответствии с расширенной аксиомой сложения P(B) = P(A) + P(B\A). Отсюда и из аксиомы неотрицательности приходим к утверждению 3. В частности, так как всегда , то с учетом аксиомы нормированности получаем утверждение 4. Поскольку , , 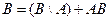то, используя расширенную аксиому сложения, находим и . Подставляя в первое из последних двух равенств вероятность ,выраженную из второго равенства, приходим к утверждению 5. Утверждение 6 можно доказать с помощью метода математической индукции по п. Так, для трех событий А, В и С

Иногда вместо аксиомы 3 удобно использовать две другие аксиомы.

Аксиома 3' (аксиома сложения): для любых попарно непересекающихся событий A₁, ..., A_n справедливо равенство

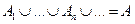Аксиома 4 (аксиома непрерывности): если последовательность событий A₁, ..., A_n, такова, что , , и , то

Определение. Тройку (Ω, B, P), состоящую из пространства элементарных исходов Ω, с σ-алгеброй событий B и определенной на B вероятности P, называют вероятностным пространством.