Фінансовий ризик

Фінансовий ризик – ризик, який виникає при здійсненні фінансового підприємства або фінансових операцій і пов’язаних з імовірністю втрат фінансових ресурсів.

Виокремлюють кілька великих груп фінансових ризиків.

1. Валютні та інвестиційні ризики, пов’язані із змінами купівельної здатності грошей.

2. Ризики фінансової стійкості, пов’язані з порушенням рівноваги фінансового розвитку підприємства або незбалансованого розвитку підприємства або незбалансованою ліквідністю його активів. Це ризики невідповідності у структурі пасивів та активів підприємства. вони охоплюють два види:

- ризик зниження фінансової стійкості. Він генерується недосконалою структурою капіталу (надто великою часткою залучених коштів), що породжує незбалансованість обсягів потоків доходів (від різних напрямів діяльності) і зобов’язань (перед банками – по кредитах, перед державою – по податках і відрахуваннях, працівниками – по заробітній платі, перед партнерами – по постачанню матеріально-енергетичних ресурсів, наданню послуг тощо);

- ризик ліквідності. Виникає за необхідності оперативного конвертування активів підприємства в готівкові кошти.

3. Кредитний ризик чи ризик неповернення боргу. Він однаково стосується всіх суб’єктів господарської діяльності. Він присутній при наданні товарного (комерційного) або споживчого кредиту покупцям. Він може набувати таких форм:

- ризик вибору недобросовісного партнера, спричинений неправильною оцінкою кредитоспроможності партнера, неповною інформованістю про його ринковий статус;

- промисловий ризик, пов’язаний з можливістю спаду виробництва чи попиту на продукцію певної галузі;

- ризик урегулювання і поставок, зумовлений невиконанням з будь-яких причин договірних зобов’язань;

- ризик, спричинений трансформацією виду ресурсів (найчастіше за терміном), втратою їх споживчої вартості для споживання або зниженням корисності використання;

- ризик форс-мажорних обставин.

4. Фінансово-інвестиційні ризики, які супроводжують інвестиційну діяльність підприємства, обтяжують досягнення запланованих цілей інвестування (прибутку або соціального ефекту)і загрожують грошовими втратами. Вони поділяються на 3 групи:

4.1. Ризик фінансових інвестицій належить до портфельних, оскільки діє на всю сукупність фінансових інвестицій (акції, облігації, ощадні (депозитні) сертифікати), якими оперує підприємство. Рівень портфельного ризику завжди нижчий, ніж рівень окремих інвестиційних інструментів, які до нього належать (за рахунок ефекту диверсифікації, коваріації тощо).

Припустимо, що маємо два ризиковані активи, що характеризуються парами «сподіваний доход – ризик» (μ ₁, σ ₁), ((μ ₂, σ ₂). Позначимо доходність першого активу через ξ;, другого – через η;. Відповідно інвестиції – через х та у.

Доход портфеля з двох ризикованих активів становитиме величину

ξ х + η у,

його сподіване значення

μ _р = μ ₁х + μ ₂у. (5.1)

значно складнішою є ситуація із ступенем ризику, або середньоквадратичним відхиленням портфеля. Річ у тім, що на відміну від математичного сподівання дисперсія суми випадкових величин не збігається з сумою дисперсій. Дисперсія визначається як Dξ = M(ξ – Mξ)².

Використовуючи його, можна визначити дисперсію суми двох величин:

D(ξ + η) = М(ξ + η - Мξ - Мη)² = Dξ + Dη + 2(Мξ η - Мξ Мη).

Неважко побачити, що дисперсія суми відрізняється від суми дисперсій на подвоєну величину Мξ η – Мξ Мη. Цявеличина називається коваріацією двох випадкових величин і позначається через cov(ξ, η).

Використовуючи поняття коваріації, можна визначити середньоквадратичне відхилення портфеля, що складається з двох ризикованих активів –

σ _р = √ D(ξ + η) = √ х² Dξ + у² Dη + 2ху cov(ξ, η). (5.2)

Використовуючи формули, можна дослідити рівновагу індивіда, що максимізує корисність портфеля на множині «ризик-сподіваний доход».

Для виміру ступеня ризикованості цінного паперу частіше використовується так званий коефіцієнт Бета – відношення коваріації доходності цінного паперу і до дисперсії доходності ринкового паперу, тобто

β _і = σ _іm / σ _m². (5.3)

Тоді лінію ринкової доходності можна записати у вигляді

μ _і = μ ₀ + β _і(μ _р - μ ₀). (5.4)

Доходність цінного паперу, розраховану за рівнянням (4.4), називають ставкою рівноваги доходності цінового паперу – і.

Фактична сподівана дохідність цінного паперу може відрізнятися від ставки рівноваги. Чим більше перевищує фактична ставка доходності ставку рівноваги, тим привабливіший для інвестора даний цінний папір. Тому лінія ринкової рівноваги розділяє множину активів у просторі «сподівана доходність – ризик» на множину привабливих та непривабливих з точки зору інвесторів.

μ і

Лінія ринкової рівноваги може зображатися графічно як функція від β (рис. 5.1).

		Коефіцієнт β

 

 

Рис. 5.1. Лінія ринкової рівноваги цінних паперів.

 

Якщо рівень ризику та дохідність акції становлять координати точки, яка міститься нижче лінії ринкової рівноваги, то вважається, що цю акцію не варто купувати (наприклад, акція Б). акція з набором координат, який забезпечує перебування точки вище лінії ринкової рівноваги, варта того, щоб до неї звернувся потенційний покупець (акція А).

4.2. Ризик окремого фінансового інвестиційного інструменту розглядають як імовірність відхилення фактичного інвестиційного доходу від очікуваної його величини за невизначеності динаміки кон’юнктури відповідного сегмента фінансового ринку і майбутніх результатів господарської діяльності його емітента (юридична особа або держава, яка випускає в обіг цінні папери, платіжно-розрахункові документи або грошові знаки і зобов’язується виконувати вимоги, що випливають з умов випуску);

4.3. Ризик реальних інвестицій (інвестиційного проекту чи проектний) виникає у процесі реалізації інвестиційного проекту за несприятливих подій, які спричинять зниження його очікуваної ефективності. Рівень ризику є вербальним внаслідок дії різноманітних об’єктивних і суб’єктивних динамічних факторів, тому необхідна індивідуальна оцінка кожного конкретного інвестиційного проекту. Першу стадію інвестиційного проекту – інвестування засобів у різні активи – супроводжують ризики незавершення проекту, проектування тощо, а другу – повернення інвестованих коштів і одержання прибутку - обтяжують ризики неокупності проекту, виробничі, комерційні тощо.

Розглянемо приклад з інвестором, що бажає своє багатство А розподілити між двома напрямками інвестицій. перший напрямок обіцяє йому гарантований доход обсягом а на одиницю інвестицій, другий – випадковий ξ;. Сподіване значення випадкового доходу позначимо через μ = Мξ;, середньоквадратичний розкид - σ;, обсяг інвестицій у безризиковий актив – х, у ризиковий – у. Отже,

Х + у = А. (5.5)

Загальний доход від інвестицій становитиме випадкову величину

ах + ξ у,

сподіваний доход

μ _р = М(ах + ξ у) = ах + μ у,

а середньоквадратичне відхилення

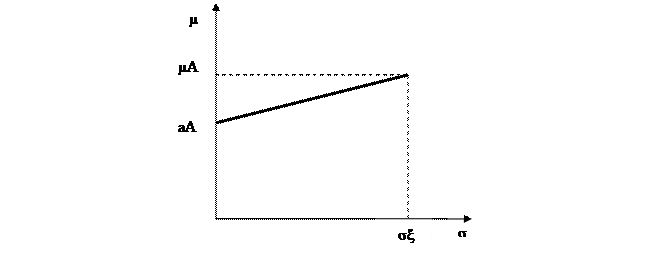
σ _р = √ D(ax + ξ у) = √ D(ax) + D(ξ у).

Беручи до уваги, що дисперсія детермінованої величини дорівнює нулю, а також те, що для детермінованої величини у: D(ξ у) = у²Dξ;, середньоквадратичний розкид інвестицій матиме вираз

σ _р = у ∙ σ ξ. (5.6)

використовуючи обсяг безризикової інвестиції та сподіваний доход можна виразити через обсяг ризикованої:

μ _р = М(а(А – у) + ξ у) = аА + (μ – а)у. (5.7)

Якщо обсяг у ризикованої інвестиції змінюється від 0 до А, то значення сподіваного доходу та середньоквадратичного розкиду утворюють відрізок у просторі «сподіваний доход – ризик» (рис. 5.2).

Рис. 5.2. Комбінації сподіваного доходу за різних обсягів інвестицій у ринковий актив

 

Якщо інвестиції здійснюють повністю у безризиковий актив (у = 0), то це відповідає точці з нульовим ступенем ризику та сподіваним доходом аА. Якщо обсяг інвестицій повністю використовується для ризикованого активу, то комбінація «ризик – сподіваний доход» має вигляд (σ ξ, μ А).

На рис.5.2 зображений випадок, коли сподівана доходність ризикованого активу перевищує доходність безризикового. Очевидно, що кутовий коефіцієнт відрізку допустимих комбінацій «ризик - сподіваний доход» дорівнює

μ – А

А.

σ ξ

 

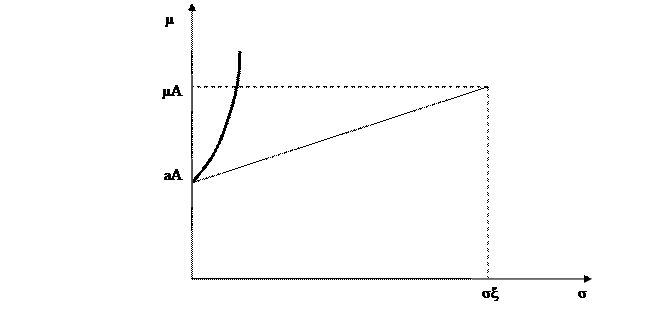
Для того щоб зрозуміти, як формується портфел інвестора, потрібно сумістити моделі бажаного (рис. 5.2) та можливого. Цей синтез відображений на рис. (5.3). На ньому показані поверхні байдужості, що містять точки найпривабливіших виборів для двох інвесторів. Точка V₁ відповідає вибору менш схильного до ризику інвестора, V₂ – більш схильного. Для першого інвестора найпривабливішим є отримання меншого сподіваного доходу при меншому ризику, порівняно з другим. Отже, інвестиції у ризикований актив будуть меншими для першого інвестора.

 

Рис. 5.3 Рівновага інвесторів з різними уподобаннями щодо ризику

 

Геометрично точка рівноваги для інвестора – це точка дотику відрізку можливих комбінацій «ризик – сподіваний доход» до поверхні байдужості у просторі «ризик – сподіваний доход». Це означає, що відрізок можливих комбінацій «ризик – сподіваний доход» є дотичною до поверхні байдужості у точці оптимального вибору. Оскільки тангенс куту нахилу відрізка, що проходить через точки (0, аА), (σ ξ, μ А) збігається з величиною (А(μ – А) / σ ξ), то рівняння рівноваги для інвестора матиме вигляд:

μ - A

MRSσ μ = ———— A. (5.8)

σ ξ

Величину (А(μ – А) / σ ξ) можна інтерпретувати як премію за ризик, оскільки вона показує, як збільшується сподіваний доход при збільшенні середньоквадратичного розкиду (ступеня ризику) на одиницю. Тому рівняння рівноваги інвестора можна прочитати таким чином: гранична норма заміни ступеня ризику сподіваним доходом інвестора у стані рівноваги збігається з премією за ризик.

Вибір на користь ризикованого чи безризикового активу залежить від уподобань індивіда щодо ризику. Проте у стані рівноваги для всіх інвесторів, що перебувають у стані рівноваги, гранична норма заміни ступеня ризику сподіваним доходом однакова.

На рис. (5.3) зображені стани рівноваги двох інвесторів, причому інвестиції у ризикований актив для обох вигідні. Можливий варіант, коли це не так. Якщо перша одиниця ступеня ризику вимагає більшого відшкодування для інвестора, ніж премія за ризик, тоді інвестиції у ризикований актив недоцільні. Ця ситуація зображена на рис. (5.4).

Рис. 5.4. Невигідність інвестицій у ризикований актив

 

Можливий також варіант, що ризикований актив настільки привабливий, що інвестору вигідно позичати або вкласти у нього суму більшу за ту, що у нього є.

5. Відсоткові ризики зумовлені небезпекою виникнення втрат у комерційних банків, кредитних установ, інвестиційних компаній внаслідок перевищення відсоткових ставок, які виплачуються за запозичені кошти, над ставками по наданих кредитах.

Фактичну ставку відсотка з урахуванням кредитного ризику можна виразити формулою:

1 + r

r_ф = ————— - 1 (5.9)

1 – p

де р – імовірність неповернення неповернення позичальником суми позики та відсотків за нею (0 ≤ р ≤ 1);

r – базова (або безризикова) відсоткова ставка (у часках одиниці).

Уточнена формула розрахунку відсоткової ставки з урахуванням інфляційного ризику має вигляд:

1 + r

r_ф = ————— - 1 + r_і (5.10)

1 – p

де r_і – надбавка за очікуване та неочікуване зростання інфляції (у частках одиниці).