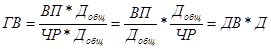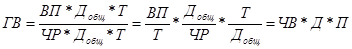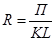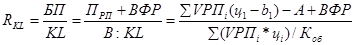Моделирование мультипликативных факторных систем в АХД

осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при ис­следовании процесса формирования объема производства продук­ции (см. рис. 3.5) можно применять следующие детерминирован­ные модели:

ВП= ЧРГВ;

П= ЧРДДВ;

ВП = ЧРДП- ЧВ.

Эти модели отражают процесс детализации исходной фактор­ной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень де­тализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Аналогичным образом, т.е. путем расчленения одного из фак­торных показателей на составные элементы, осуществляется мо­делирование аддитивных факторных систем.

Как известно, объем реализации продукции равен

УРП= УВП-0_н.п,

где УВП — объем выпуска продукции;

О_цп — остатки нереализованной продукции.

Часть нереализованной продукции может находиться на складах предприятия (О_т), а часть может быть отгружена покупателям, но еще не оплачена (О_от). Тогда приведенную исходную модель мож­но записать следующим образом:

УРП = УВП-0_скл -О_отг.

 

К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расшире­ния и сокращения.

Метод удлинения предусматривает удлинение числителя исход­ной модели путем замены одного или нескольких факторов на сум­му однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (3) и объема выпуска продукции (VВП). Исходная модель этой факторной системы будет иметь следующий вид:

С=

 

Если общую сумму затрат (3) заменить отдельными их элемен­тами, такими, как заработная плата (ЗП), материальные затраты (МЗ), амортизация основных средств (А), накладные расходы (HP) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:

ЗП МЗ A HP

С=––––– +–––––– +–––––+–––––– х₁ + х₂ + х₃ + х₄,

УВП УВП УВП УВП '

где х₁ — трудоемкость продукции;

х₂ — материалоемкость продукции; х₃ — фондоемкость продукции;

х₄ — уровень накладных расходов.

Способ формального разложения факторной системы предусмат­ривает удаинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведе­ние однородных показателей.

Если Ь = 1 + т + п + р, то

	Y=

 

В результате получили конечную модель кратно-аддитивного вида с новым набором факторов. На практике такое разложение встречается довольно часто. Например, при анализе показателя рентабельности производства (R):

,

где П — сумма прибыли от реализации продукции;

3 — сумма затрат на производство и реализацию "продукции.

Если сумму затрат заменить на отдельные ее элементы, конеч­ная модель в результате преобразования приобретет следующий вид:

Метод расширения предусматривает расширение исходной фак­торной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в ис­ходную модель

 

 

ввести новый показатель с, то модель примет следующий вид: _г

 

 

В результате получается конечная мультипликативная модель в виде произведения нового набора факторов.

Этот способ моделирования очень широко применяется в ана­лизе. Например, среднегодовую выработку продукции одним ра­ботником (показатель производительности труда) можно записать таким образом:

 

 

Если ввести такой показатель, как количество отработанных дней всеми работниками (Добщ), то получим следующую модель го­довой выработки:

 

 

где ДВ — среднедневная выработка;

Д — количество отработанных дней одним работником. После введения показателя количества отработанных часов все­ми работниками (Г) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (77):

Метод сокращения представляет собой создание новой фактор­ной модели путем деления числителя и знаменателя дроби на один и тот же показатель:

 

 

 

 

В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.

Например, рентабельность операционного капитала рассчиты­вается делением суммы прибыли от реализации продукции (П) на среднегодовую стоимость основного и оборотного капитала пред­приятия (KL)

Если числитель и знаменатель разделить на выручку от реали­зации продукции (В), то получим кратную модель, но с новым на­бором факторов — рентабельности продаж и капиталоемкости продукции:

 

Необходимо заметить, что на практике для преобразования од­ной и той же модели может быть последовательно использовано несколько методов. Например, процесс создания факторной мо­дели рентабельности совокупного капитала (R_KL) можно предста­вить следующим образом:

 

где БП — общая сумма брутто-прибыли за отчетный период до

выплаты процентов и налогов;

KL — среднегодовая сумма совокупного капитала;

П_рп — прибыль от реализации продукции (услуг);

ВФР– внереализационные финансовые результаты;

В — выручка от реализации продукции (услуг);

VРП. — объем реализации продукции /-го вида в натуральном

выражении;

ц — отпускные цены на i -й вид продукции;

b_i— прямые производственные затраты на единицу /-го вида

продукции;

А — косвенные затраты периода;

К_об — коэффициент оборачиваемости совокупного капитала, за отчетный период (отношение выручки к среднегодовой

сумме капитала).

В данном случае для преобразования исходной факторной мо­дели, построенной на математических зависимостях, использо­ваны способы удлинения и расширения. В результате получилась более содержательная модель мультипликативно-аддитивно-крат­ного вида, которая имеет большую познавательную ценность, поскольку учитывает причинно-следственные связи между пока­зателями. Данная модель позволяет исследовать, как влияют на доходность капитала объем продаж, отпускные цены, себесто­имость реализованной продукции, внереализационные финан­совые результаты, а также скорость оборота капитала.

Таким образом, результативные показатели могут быть разло­жены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моде­лей. Выбор способа моделирования зависит от объекта исследова­ния, от поставленной цели, а также от профессиональных знаний и навыков исследователя.

Процесс моделирования факторных систем — очень сложный и ответственный момент в АХД. От того, насколько реально и точ­но созданные модели отражают связь между исследуемыми пока­зателями, зависят конечные результаты анализа.

Вопросы для контроля знаний

3. Что собой представляет метододерм АХД? Каковы ее харак­терные черты?

2. Что означает системный подход и ситуационный подходов АХД?

3. Что представляет собой методика АХД?

4. Каковы основные технологические этапы выполнения анали­тической работы?

5. Каковы основные приемы, используемые в АХД?¹ По каким признакам они классифицируются?

6. Какие основные классификационные группы показателей вы знаете?

7. Каковы основные подсистемы комплексного экономического анализа?

8. Какова последовательность изучения показателей?

9. Что понимается под факторным анализом? Каковы его задачи?

10. Что такое детерминированный и стохастический факторный анализ?

Что такое прямой и обратный факторный анализ? Какой из них имеет большее значение?

Что такое ретроспективный и перспективный факторный анализ?

Каковы основные виды классификации факторов в АХД? Для чего производится систематизация факторов? Как созда­ется детерминированная факторная система? Что представляет собой моделирование факторных систем? Какие основные типы факторных моделей применяются в детерминированном анализе?

Как производится преобразование факторных моделей мето­дами расширения, удлинения, сокращения?
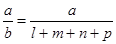