Основные законы динамики
ДИНАМИКА ТОЧКИ Методические указания для студентов очного обучения
Ростов на-Дону
УДК 531.01
Динамика точки: Методические указания для студентов очного обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2007.- 16 с.
Предназначены для студентов очного отделения РГСУ. Даны основные определения, формулировки теорем, разъясняются трудные для усвоения понятия. Рассмотрены типовые задачи. УДК 531.01
Составитель: канд.физ.-мат. наук О.В. Явруян
Редактор Т.М. Климчук Темплан 2007 г., поз.155
Подписано в печать 31.05.07.Формат 60´84/16. Бумага писчая. Ризограф. Уч.-изд. л. 1,3. Тираж 50 экз. Заказ 323.
Редакционно-издательский центр Ростовского государственного строительного университета 344022, Ростов-на-Дону, ул. Социалистическая, 162
©Ростовский государственный строительный университет, 2007
ДИНАМИКА ТОЧКИ
Основные законы динамики
Динамика представляет собой часть кинетики, посвященную изучению движения материальных тел (или вообще механических систем) в зависимости от действующих на них сил. Движение тела определяется движением всех материальных точек (или частиц), его составляющих; поэтому естественно начать изучение динамики с изучения движения материальной точки. Под материальной точкой мы понимаем тело столь малых размеров, что различием в движении его частиц можно пренебречь. Материальную точку можно рассматривать как точку (геометрическую), имеющую массу. В дальнейшем часто для краткости материальную точку будем называть просто точкой. В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном[1] в его классическом сочинении «Математические начала натуральной философии», изданном в 1687 г. Первый закон (закон инерции), открытый Галилеем (1638 г.), гласит: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции. Закон инерции отражает одно из основных свойств материи — пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=Q, то точка покоится или движется с постоянной по модулю и направлению скоростью (v = const); ускорение точки при этом равно нулю (w = Q); если же движение точки не является равномерным и прямолинейным, то на точку действует сила. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). По данным опыта, для нашей Солнечной системы инерциальной является система отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей. Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы. Он гласит: производная по времени от количества движения материальной точки равна действующей на нее силе. Другая ее формулировка: произведение массы материальной точки на ее ускорение равно действующей на точку силе.
Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот. Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т. е. равнодействующей R, равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
Этот же результат можно получить, используя вместо аксиомы параллелограмма закон независимости действия сил, согласно которому при одновременном действии на точку нескольких сил каждая из них сообщает точке такое же ускорение, какое она сообщила бы, действуя одна. Вес тела и его масса. На все тела, находящиеся вблизи земной поверхности, действует сила тяжести Р, численно равная весу тела. Опытом установлено, что под действием силы Рлюбое тело при свободном падении на Землю (с небольшой высоты и в безвоздушном пространстве) имеет одно и то же ускорение g. Это ускорение, сообщаемое телу силой тяжести, называют для краткости ускорением силы тяжести, или ускорением свободного падения. Для этого движения на основании уравнения (2) имеем: P=mg или m = Равенство (3) позволяет определить вес тела, если известна его масса, и наоборот; оно устанавливает, что вес тела равен его массе, умноженной на ускорение силы тяжести, или масса тела равна его весу, деленному на ускорение силы тяжести. Вес тела, как и величина g, изменяется с изменением широты и высоты над уровнем моря; масса же является величиной, для данного тела (или материальной точки) неизменной.
|

 . (1)
. (1)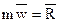 или
или 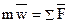 . (2)
. (2)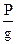 (3)
(3)


