Решение второй (основной) задачи динамики
Эта задача состоит в том, чтобы, зная действующую силу F, найти закон движения точки, т. е. кинематические уравнения (6). Сила Fможет
Нахождение закона движения данной точки сводится к интегрированию системы (7), т. е. системы трех совместных дифференциальных уравнений второго порядка, в которых неизвестными функциями являются координаты движущейся точки х, у, z, а аргументом - время t. Проинтегрировав эту систему дифференциальных уравнений, получим х, у, zв функциях времени и шести произвольных постоянных, т. е. найдем общее решение (общие интегралы) системы (7) в виде
Наличие в правых частях уравнений (8) произвольных постоянных указывает на то, что под действием данной силы точка может совершать не какое-то вполне определенное движение, а целый класс движений, имеющих разные законы при разных значениях постоянных Ci, i=1..6. Физически этот результат объясняется тем, что точка, на которую начинает действовать некоторая сила, будет двигаться по-разному в зависимости от так называемых начальных условий, т. е. от начального положения и начальной скорости этой точки. Например, движение свободной материальной точки под действием силы тяжести может быть прямолинейным или криволинейным в зависимости от направления ее начальной скорости. Чтобы сделать соответствующую задачу динамики определенной, надо кроме действующих сил задать начальные условия, т. е. для некоторого момента времени t = t0(начальный момент) задать: начальное положение точки и начальную скорость точки
|

 . Поэтому дифференциальные уравнения (5) будут в общем случае иметь следующий вид:
. Поэтому дифференциальные уравнения (5) будут в общем случае иметь следующий вид: (7)
(7)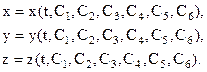 (8)
(8)




