Используя поверхностный интеграл первого рода, найти площадь S указанной части заданной поверхности.
| № вар.
| 7.1
|
|
| полусфера 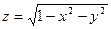
|
|
| часть параболоида х2 + у2 = 6 z, заключенная внутри цилиндра х2+у2 = 27
|
|
| часть параболоида 1 – z = x2 + y2, 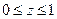
|
|
| часть конуса x2 + у2 = 3 z2, 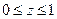
|
|
| полусфера 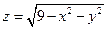
|
|
| усеченный конус 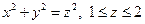
|
|
| часть параболоида  , , 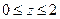 , ,
|
|
| сечение цилиндра 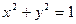 плоскостью плоскостью 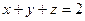
|
|
| часть поверхности конуса  , расположенная в первом октанте между плоскостями , расположенная в первом октанте между плоскостями  и и 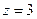
|
|
| шаровой сегмент 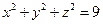 , , 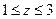
|
|
| часть параболоида  , расположенная между цилиндрами , расположенная между цилиндрами 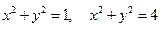
|
|
| шаровой слой: 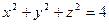 , , 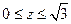
|
|
| шаровой сегмент 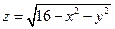 , , 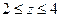
|
|
| поверхность 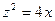 , расположенная в первом октанте и вырезанная поверхностями , расположенная в первом октанте и вырезанная поверхностями  и и 
|
|
| часть поверхности конуса  , расположенная в первом октанте между плоскостями , расположенная в первом октанте между плоскостями  и и 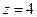 . .
|
|
| часть поверхности параболоида  , заключенной между цилиндрами , заключенной между цилиндрами 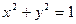 , , 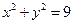 . .
|
|
| часть поверхности 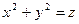 , вырезанная цилиндрами , вырезанная цилиндрами 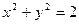 , , 
|
|
| часть поверхности конуса 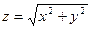 , отсеченная поверхностями , отсеченная поверхностями 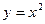 , , 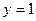 . .
|
|
| часть цилиндра  , заключенная внутри другого цилиндра , заключенная внутри другого цилиндра 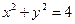
|
|
| часть поверхности конуса  , , 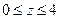
|
|
| часть поверхности конуса 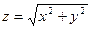 , отсеченная поверхностями , отсеченная поверхностями 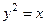 , , 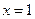
|
|
| часть параболоида  , , 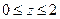
|
|
| часть параболоида 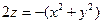 , , 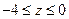
|
|
| часть поверхности конуса 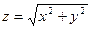 , отсеченная поверхностями , отсеченная поверхностями 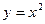 и и 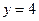
|
|
| часть параболоида 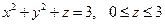
|
|
| часть полусферы
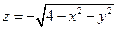 , , 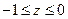
|
|
| часть параболоида 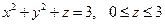 , расположенная в первом октанте , расположенная в первом октанте
|
|
| часть конуса
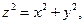 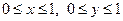
|
|
| часть параболоида 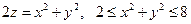
|
|
| часть полусферы

|