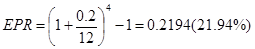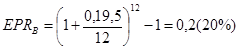Сущность и методический инструментарий компаундирования денежных потоков

Принятие и обоснование любого управленческого решения прямо или косвенно связано с финансовыми потоками (поступле­нием и расходованием денежных средств), поэтому каждый менед­жер, ответственный за принятие финансовых решений, должен хорошо владеть техникой финансовых вычислений, понимать и уметь применять математический аппарат, который используется в финансовом анализе.

Финансовые вычисления имеют давнюю историю и относятся к традиционным методам исследования денежных потоков, осно­ванным на концепции нарашения сложных процентов (compoun­ding) или дисконтирования денежных поступлений, учитывающим изменение стоимости денег во времени, неравноценность совре­менных и будущих благ.

Связь стоимости денег со временем проявляется в существовании процента, уплачиваемого за выгоду раннего использования денеж­ных средств или получаемого в виде вознаграждения за воздержа­ние от немедленного их потребления. Согласно теории предпоч­тения ликвидности и предпочтения текущих потребностей людям свойственно потреблять сегодня в противовес потреблению в бу­дущем. Они могут отказаться от немедленного потребления только в надежде повысить его будущий уровень благодаря процентным доходам. Проценты компенсируют заимодавцу потери потенци­альной выгоды при альтернативном использовании денежных средств, а ссудозаемшик платит за дополнительную выгоду ранне­го потребления этих средств, которые в противном случае ему при­шлось бы долго накапливать.

Сегодняшние деньги всегда дороже будущих — и не только по причине инфляции. Если инвестор получит доход сегодня, то он может пустить деньги в оборот, к примеру положить в банк на де­позит, и заработать определенную сумму в виде банковского про­цента. Если же этот доход он получит через несколько лет, то по­теряет такую возможность.

151

Сущность метода компаундинга — определение суммы денег, которую будет иметь инвестор в конце финансовой операции. При этом исследование денежного потока ведется от настоящего к бу­дущему. Заданными величинами являются исходная сумма инвес­тиций, срок и процентная ставка доходности, а искомой величи­ной — сумма средств, которая будет получена после завершения операции.

Начисление сложных процентов производится в конце каждого периода на основную сумму долга с добавлением начисленных процентов, не востребованных инвестором, за предыдущие пери­оды.

Если бы нам нужно было вложить на три года 1000 тыс. руб. в банк, который выплачивает 20% годовых, то мы рассчитали бы следующие показатели доходности:

за первый год: 1000 (1 + 20%) = 1000 ■ 1,2 = 1200 тыс. руб.;

за второй год: 1200 (1 + 20%) = 1200 ■ 1,2= 1440 тыс. руб.;

за третий год: 1440(1 +20%)= 1440- 1,2= 1728 тыс. руб.

Это можно записать и таким образом:

1000- 1,2- 1,2-1,2= 1000- 1,2³ = 1728 тыс. руб.

Из данного примера видно, что 1000 тыс. руб. сегодня равно­ценна 1728 тыс. руб. через три года. Напротив, 1728 тыс. руб. дохо­да через три года эквивалентны 1000 тыс. руб. на сегодняшний день при ставке рефинансирования 20%.

Данный пример показывает методику определения стоимости инвестиций при использовании сложных процентов. Сумма го­довых процентов каждый год возрастает в геометрической про­грессии, так как мы имеем доход как с первоначального капи­тала, так и с процентов, полученных за предыдущие годы.

Поэтому для определения стоимости, которую будут иметь ин­вестиции через несколько лет, при использовании сложных про­центов применяют формулу

FV=PV(\ + r)>;,

где FV— будущая стоимость инвестиций через п лет; PV— первоначальная сумма инвестиций; г — ставка процента в виде десятичной дроби; / — число лет в расчетном периоде.

Выражение (1 + г) является важной переменной в финансовом анализе, составляет основу практически всех финансовых вычис­лений. Оно показывает, сколько будет стоить денежная единица

через год. Обратное его значение 1/(1 + г) позволяет определить, сколько сегодня стоит денежная единица, которая будет получена через год.

При начислении процентов по простой ставке используется сле­дующая формула:

/У= PV{\ + /я) = 1000 ■ (1 + 0,2 • 3) = 1600 тыс. руб.

На рис. 7.1 сопоставляется будущая стоимость 1 руб. инвести­ций, вложенных под простые и сложные проценты. Ставка в обоих случаях равна 20% годовых. В случае простых процентов график прямолинейный, а в случае сложных — растет по экспоненте, и расстояние между кривыми со временем увеличивается. Этот разрыв объясняется тем, что в первом случае начисление процен­тов производится от неизменной базы (начисленные проценты каждый раз инвестором изымаются), а во втором случае — от воз­росшей суммы инвестиций с учетом капитализированных процен­тов.

1,6

1,4 1,2

1,0. ---------------------- 1-------------------------,---------------

0 12 3

Рис. 7.1. Будущая стоимость 1 руб., вложенного под 20% годовых под простые и сложные проценты

Вместе с тем для вкладчика более выгодной является схема про­стых процентов, если срок вклада менее одного года и проценты начисляются однократно в конце периода. Напротив, более выгод­ными являются вклады под сложные проценты, если срок вклада превышает один год. Оба вида процентов обеспечат одинаковые доходы, если срок вклада составит один год (при условии одно­кратного их начисления).

Для подтверждения сказанного рассчитаем наращенную сумму вклада с исходной суммы, равной 500 тыс. руб., по ставке простых

 

152

153

1,8-

1,6-

1,4-

1,2 -

и сложных процентов для разных временных интервалов из расче­та 24% годовых (табл. 7.1).

Таблица 7.1 Расчет наращенной суммы вклада по ставке простых и сложных процентов

 

 

Вид процентов	Период начисления процентов
90 дней (t=1/4)	270 дней (t = 3/4)	1 год (t=1)	Згода	5 лет (t = 5)
Простые
Сложные	527,6	587.5		953,3	1465,8

При оценке стоимости денег во времени по сложным процентам необходимо учитывать не только уровень объявленной ставки про­цента, но и количество интервалов начисления процентов в течение года. Если доходы по инвестициям начисляются несколько раз в год по ставке сложных процентов, то формула для определения буду­щей стоимости вклада имеет следующий вид:

FV=PV(\ +r/m)^!m,

где т — число периодов начисления процентов в году.

Допустим, в вышеприведенном примере проценты начисляют­ся ежеквартально (т = 4, t = 3). Тогда будущая стоимость вклада через 3 года составит

FV= 1000 ■ (1 + 0,2/4)¹² = 1000 ■ 1,79585 = 1795,85 тыс. руб.

Дополнительные 67,85 тыс. руб. (1795,85 — 1728) возникли бла­годаря тому, что сложные проценты начислялись не 3 раза, а 12 раз.

Чем чаще начисляются проценты, тем быстрее растет вклад. При ежемесячном начислении процентов через 3 года мы получим следующий доход:

FV= 1000 ■ (1 + 0,2/12)³⁶ = 1000 ■ 1,81313 = 1813,13 тыс. руб.

Поэтому иногда выгоднее инвестировать средства под меньший процент, но с более частым его начислением.

На рис. 7.2 сопоставлены кривые, отображающие приращение стоимости вклада, вложенного под 20% годовых, с ежегодным и ежемесячным начислением процентов.

В связи с этим возникает необходимость сравнения условий финансовых операций, предусматривающих различные периоды начисления процентов.

Рис. 7.2. Будущая стоимость 1 руб., вложенного под 20% годовых, начисляемых ежегодно и ежемесячно

Приведение соответствующих номинальных (фиксированных) процентных ставок к их годовому эквиваленту производится по сле­дующей формуле:

EPR - (1 + -)^т - 1, т

где EPR — эффективная ставка процента (ставка сравнения);

г — ставка процента;

т — число периодов начисления.

В нашем примере эквивалентная ставка процента будет равна: а) при ежеквартальном начислении процентов:

 

б) при ежемесячном начислении процентов:

 

в) при ежедневном начислении процентов:

 

Вычисляя EPR, мы получаем возможность сравнивать процент­ные ставки по ссудам или инвестициям с разными периодами на­числения процентов. Например, банк А платит по депозитам 20% годовых с полугодовым начислением процентов, банк В — 19,5% с ежемесячным начислением процентов. Нужно определить, куда

 

154

155

выгоднее помещать денежные вклады. Для этого рассчитаем эф­фективные ставки процента: • для банка А:

Упростить данную процедуру расчета общей суммы причита­ющегося процента можно, применив следующую формулу:

К СП я+1 12 ' 2

Проц =

- 4575 долл.,

05000-12% 60+_P 12

где К — сумма полученного кредита;

СП — годовая ставка процента по кредиту; п — количество интервалов начисления платежей и процен­тов.

 

Следовательно, выгоднее хранить деньги во втором банке. Если известны величины FV, РУ и /, то можно определить про­центную ставку по следующей формуле:

 

Зная FV, PVh /*, можно определить длительность операции:

 

Часто возникает необходимость определения суммы процента по долгосрочным кредитам, выплачиваемого равномерными частями в течение определенного периода. Предположим, вы получили кредит на строительство жилья в сумме 15 000 долл. на пять лет под 12% годовых, который вы будете выплачивать ежемесячно. Следователь­но, вам предстоит произвести 60 платежей по 250 долл. плюс про­центы, которые будут начисляться на убывающую сумму долга:

 

Порядковый номер платежа	Сумма платежа по кредиту	Сумма процента по кредиту	Общая сумма платежа	Остаток долга после погашения
		150,0	400,0	14 750
		147,5	397,5	14 500
		145,0	395,0	14 250
		142,5	392,5
		5,0	255,0
		2,5	252,5	-
Итого	15 000		19 575	-

Общую сумму причитающегося процента (Проц) можно рассчи­тать таким образом:

150 + 2,5

Проц =

- 2 60 = 4575 долл.