
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ПОРЯДОК
Дата добавления: 2015-10-18; просмотров: 620
|
|
Определение. Функция  называется бесконечно малой при
называется бесконечно малой при 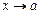 или
или 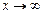 , если
, если 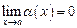 или
или  .
.
Например, 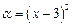 бесконечно малая при
бесконечно малая при  ;
;  - бесконечно малая при
- бесконечно малая при 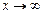 .
.
Функция  называется бесконечно большой величиной при
называется бесконечно большой величиной при 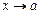 или
или 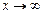 , если для нее выполняются условия
, если для нее выполняются условия 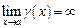 или
или  .
.
Например,  при
при  ;
;  при
при 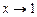 .
.
Пусть 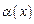 и
и 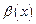 - бесконечно малые при
- бесконечно малые при 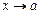 .
.
1. Если  , то
, то  является бесконечно малой высшего порядка по сравнению с
является бесконечно малой высшего порядка по сравнению с  ,
,  .
.
2. Если  , где m – число, отличное от нуля, то
, где m – число, отличное от нуля, то  и
и  - бесконечно малые одного порядка. В частности, если
- бесконечно малые одного порядка. В частности, если  , то
, то  и
и  - эквивалентные бесконечно малые,
- эквивалентные бесконечно малые,  ~
~  .
.
3. Бесконечно малая  называется бесконечно малой k- го порядка относительно бесконечно малой
называется бесконечно малой k- го порядка относительно бесконечно малой  ,если
,если  и
и  - бесконечно малые одного порядка, т. е. если
- бесконечно малые одного порядка, т. е. если 
 =А
=А  0.
0.
Таблица эквивалентных бесконечно малых:
1)  ~
~  ,
,  →0;
→0;
2) 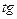
 ~
~  ,
,  →0;
→0;
3)  ~
~  ,
,  →0;
→0;
4)  ~
~  ,
,  →0;
→0;
5) 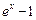 ~
~  ,
,  → 0;
→ 0;
6)  ~
~  ,
,  →0;
→0;
7)  ~ α
~ α  ,
,  →0;
→0;
8)  ~
~  ,
,  →0;
→0;
9)  ~
~  ,
,  →0.
→0.
Пример 1. Найти 
 =
=  =
= 
Пример 2. Найти 
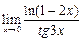
Так как  х → 0, то 3
х → 0, то 3  → 0, (- 2
→ 0, (- 2  ) → 0, поэтому
) → 0, поэтому

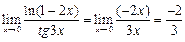
Пример 3. Найти 
Воспользуемся теоремами:
1) Алгебраическая сумма конечного числа бесконечно малых величин эквивалентна сумме части слагаемых, имеющих низший порядок малости.
2) Предел частного двух бесконечно малых величин равен пределу частного двух соответственно эквивалентных бесконечно малых величин.
1 - cos  ~
~  ; ln(l + З
; ln(l + З  ) ~З
) ~З  ; sin2
; sin2  ~
~  2;
2;  -1 ~ tg
-1 ~ tg  2 ~
2 ~  2
2
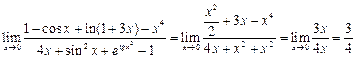 .
.
Пример 4. Сравнить бесконечно малые величины  =sin2
=sin2  и
и  = 2
= 2  sin
sin  при
при  →0,
→0,

Таким образом, α=0(β), α является бесконечно малой высшего порядка по сравнению с β.
Пример 5. Сравнить 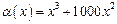 и
и 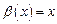 при
при 

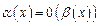 .
.
Существует конкретное число k, когда 
 при k=2,
при k=2, 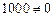 ,
,  , следовательно,
, следовательно, 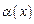 - бесконечно малая величина второго порядка по сравнению с
- бесконечно малая величина второго порядка по сравнению с 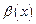 .
.
Пример 6. Доказать, что при  →1 бесконечно малые величины α(
→1 бесконечно малые величины α(  ) = (1-
) = (1-  ) и β(
) и β(  )=1-
)=1-  будут одного порядка малости.
будут одного порядка малости.
α(  ) и β(
) и β(  ) будут одного порядка малости, если тогда
) будут одного порядка малости, если тогда 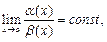 тогда
тогда

Следовательно, α(  ) и β(
) и β(  ) одного порядка малости.
) одного порядка малости.
Пример 7. Сравнить бесконечно малые величины  и
и  при
при  →0.
→0.
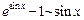 , т. к. при
, т. к. при  →0
→0 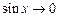 ;
;
 ;
;
 .
.
Таким образом,  , следовательно, α(
, следовательно, α(  ) и β(
) и β(  ) – эквивалентны.
) – эквивалентны.
Пример 8. Сравнить бесконечно малую величину  с бесконечно малой
с бесконечно малой  (
(  )=
)=  при
при  →0.
→0.

Тогда, 
Таким образом, α=0(β), α является бесконечно малой высшего порядка по сравнению с β.
Задания для самостоятельной работы.
Вычислить пределы, пользуясь эквивалентными бесконечно малыми величинами:
1)  2)
2) 
3) 
4) 
5) 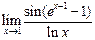
Сравнить бесконечно малые величины при  →0:
→0:
6) sin  +tg2
+tg2  и 3
и 3  ; 7)
; 7) 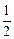 tg2
tg2  +3
+3  2 и
2 и 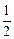
 +
+  2;
2;
8) ln(l +  2) и arcsin (
2) и arcsin (  ) ; 9)
) ; 9)  -1 и хlna;
-1 и хlna;
10) Сравнить  и
и  при
при 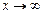 ;
;
11) При каких х функции будут бесконечно малыми?
a)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
12) При каких х функции будут бесконечно большими?
a)  ; б)
; б) 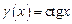 ;
;
в)  ; г)
; г)  .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Про виконання контракту і відшкодування моральної шкоди | | | Прикінцеві положення |