
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Прикінцеві положення
Дата добавления: 2015-10-18; просмотров: 807
|
|
Функция 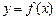 называется непрерывной в точке а, если
называется непрерывной в точке а, если
1) эта функция определена в некоторой окрестности точки а;
2) существует предел 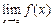 ;
;
3) этот предел равен значению функции в точке а, т.е. 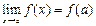 .
.
Обозначая  - а =Δx и f(x)- f(a) =Δy, условие непрерывности можно записать так:
- а =Δx и f(x)- f(a) =Δy, условие непрерывности можно записать так: 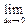 Δy = 0.
Δy = 0.
Если функция непрерывна в каждой точке некоторой области, то она непрерывна в этой области.
Точка а, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции.
Если существуют конечные пределы 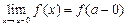 и
и 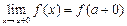 , причем не все три числа f(a), f(a - 0), f(a + 0), равны между собой, то а называется точкой разрыва I рода.
, причем не все три числа f(a), f(a - 0), f(a + 0), равны между собой, то а называется точкой разрыва I рода.
Точки разрыва I рода подразделяются на точки устранимого разрыва (когда f(a-0) = f(a + 0)≠ f (a )) и точки скачка (когда f(a - 0) ≠ f(a + 0)), f(a + 0)-f(a-0)) - скачок функции в точке а. Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов.
Пример 1. Доказать, что функция 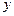 = З
= З  -4 непрерывна в точке
-4 непрерывна в точке 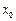 =2.
=2.
Область определения нашей функции D(f) = (- 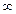 ;+
;+ 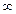 ) ,
) , 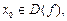 следовательно функция определена в точке x0 и в окрестности точки
следовательно функция определена в точке x0 и в окрестности точки 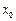 .
.
f(2) = 2, 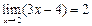
Условие 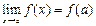 выполнено, следовательно, данная функция непрерывна в точке
выполнено, следовательно, данная функция непрерывна в точке 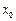 =2.
=2.
Пример 2. Доказать, что функция 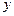 = 7
= 7  2 -3 непрерывна на интервале (-
2 -3 непрерывна на интервале (- 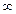 ;+
;+ 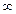 ).
).
Для доказательства непрерывности функции на (- 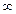 ;+
;+ 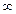 ) надо доказать непрерывность ее в произвольной точке х
) надо доказать непрерывность ее в произвольной точке х 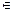 (-
(- 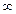 ;+
;+ 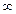 ), надо доказать
), надо доказать 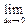 Δy = 0.
Δy = 0.
Область определения нашей функции - вся числовая ось.
Δf= f(x + Δх)- f(x) = (7(  + Δ
+ Δ  )2 -3)-(7
)2 -3)-(7  2 - 3) = 7х2 + 14хΔх +
2 - 3) = 7х2 + 14хΔх +
+ 7 Δ  2 - 3 - 7х2 + 3 = 14
2 - 3 - 7х2 + 3 = 14  Δ
Δ  + 7Δ
+ 7Δ  2 = 7Δ
2 = 7Δ  (2
(2  + Δх)
+ Δх)
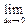 Δy =
Δy = 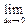 7Δ
7Δ  (2
(2  + Δх) = 0
+ Δх) = 0
Следовательно, f(x)=7x2-3 непрерывна в любой точке интервала 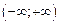 и тогда непрерывна на всем интервале.
и тогда непрерывна на всем интервале.
Пример 3. Исследовать на непрерывность функцию
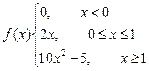

Рис. 7
Всякая элементарная функция непрерывна в своей области определения. Данная функция задается различными формулами на разных участках, следовательно, не является элементарной.
Однако, если разбить область определения D(f)= 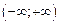 на отдельные интервалы D1(f) =
на отдельные интервалы D1(f) = 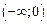 ; .D2(f) =
; .D2(f) = 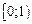 ; D 3(f)=
; D 3(f)= 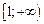 ,то на каждом из этих интервалов функция f(x) окажется элементарной и, следовательно, непрерывной.
,то на каждом из этих интервалов функция f(x) окажется элементарной и, следовательно, непрерывной.
Таким образом, осталось исследовать граничные точки.
1) x1 =0, f(x1)= f(x2)=0
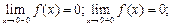
Таким образом, в точке х1, функция непрерывна.
2) 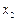 = 1
= 1
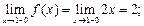
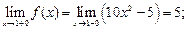
Пределы слева и справа в точке  2 не равны между собой, таким образом, точка
2 не равны между собой, таким образом, точка  2 - точка разрыва 1 рода.
2 - точка разрыва 1 рода.
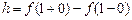 =5-2=3- скачок функции в точке
=5-2=3- скачок функции в точке  2 .
2 .
Пример 4. Найти и классифицировать точки разрыва функции y= 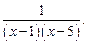
В точках  =1 и
=1 и  =5 функция не определена.
=5 функция не определена.
1)  = 1
= 1
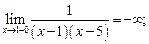
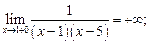
2)  =5
=5
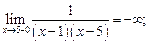
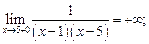
Обе точки  =1 и
=1 и  =5 - точки разрыва II рода.
=5 - точки разрыва II рода.
Пример 5. Показать, что при х=3 функция у = 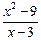 имеет устранимый разрыв.
имеет устранимый разрыв.
В точке ,  =3 функция не определена. В других точках дробь можно сократить на
=3 функция не определена. В других точках дробь можно сократить на  -3≠0, следовательно, у = х + 3 во всех точках х≠З,
-3≠0, следовательно, у = х + 3 во всех точках х≠З,
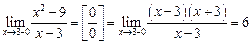
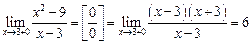
Функция в точке  =3 имеет устраняемый разрыв.
=3 имеет устраняемый разрыв.
Он будет устранен, если условиться, что при  =3 значение функции равно 6.
=3 значение функции равно 6.
Задания для самостоятельной работы.
1) Исследовать на непрерывность f(x)= 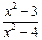 точке
точке  0=2;
0=2;
2) Доказать непрерывность функции f(x) =  + ln(l + х) в области (-1;+оо);
+ ln(l + х) в области (-1;+оо);
3) Исследовать на непрерывность функцию:
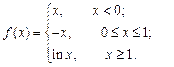
4) Исследовать характер точки разрыва функции
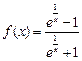 ;
;
5)Найти точки разрыва: а) 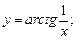 б)
б) 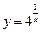 .
.
Список литературы
1.Пискунов Н.С. Дифференциальное и интегральное исчисления – М.: “ Интеграл-пресс ”,1997-416с.
2.Данко П.Е. и др. Высшая математика в задачах и упражнениях. Ч.1./ П.Е. Данко и др. – М.: Высшая школа, 1986 – 306 с.
Учебное издание
| <== предыдущая лекция | | | следующая лекция ==> |
| ПОРЯДОК | | | КОНВЕНЦІЯ про захист прав людини і основоположних свобод |