Способи задання функції

Дата добавления: 2014-10-22; просмотров: 5046

Функціяy = f(x) буде задана коли:

1) задано область xвизначення функції, тобто множину зміни аргументу x;

2) задано закон (правило), за яким встановлюється відповідність між елементами x і y.

У математиці існує чотири способи задання функцій.

Аналітичний спосіб. Це такій спосіб, коли функціональну залежність між х іy можна виразити за допомогою деякого аналітичного виразу або формули. Ця формула і вказує на те, які дії (завдання, віднімання, множення, ділення, піднесення до ступеня, добування кореня, логарифмування, знаходження значень тригонометричних функцій тощо) і в якому порядку треба виконати над сталими числами і аргументом х, щоб для кожного його значення дістати цілком певне одне значення у.

Приклади функцій, які ми наводили, це і є аналітично задані функції.

Іноді функцію можна гадати кількома формулами. Так, наприклад,

y = =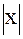

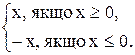
Цю функцію задамо двома формулами: для x > 0 її задаємо формулою y = x, а для x<0 – формулоюy = –x.

Зазначимо, що при цьому ми маємо одну функцію, але на різних проміжках вона задається різними формулами.

Кожний аналітичний вираз, який містить х, має свою область існування– це сукупність допустимих дійсних значень х, при яких заданий вираз набуває дійсних значень. Тому для функцій, які задано аналітично, розрізняють область визначення функції і область її існування.

Під областю існування аналітично заданої функції розуміють область існування відповідного аналітичного виразу. Проте в тих випадках, коли величини, які містяться в аналітичному виразі, мають певні фізичний або геометричний зміст, область існування функції може не збігатись з областю її визначення.

Приклад 4.Якщо через хпозначити радіус круга, а через у – його площу, то матимемо функціональну залежність, яка виразиться формулою:

у = π х²

Тут область визначення функції є множина всіх додатних дійсних чисел, а область існування функції – вся множина дійсних чисел. Функція може бути задана в інтервалі [а;b] або на відрізку.

Словесний спосіб. Часто закон відповідності між елементами двох множин описується за допомогою слів. Такий спосіб задавання функції називається словесним.

Прикладом такої функції може бути функціяу = sgn(x) (від латинського слова signum (“сигнум”), що означає “знак”).

Ця функція задається так: y = sgn(x) =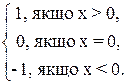

Тут кожному числу х>0 ставиться у відповідність число 1, числу х = 0 – число нуль і кожному числу х<0 – число – 1. Отже, кожному дійсному числу ставиться у відповідність одне дійсне число.

Графічний спосіб. Функцію можна задати також графічно. Справді, візьмемо Декартову систему координат (мал.1).

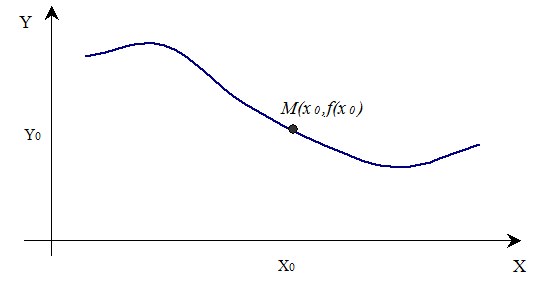
Мал.1

Тоді для кожного значення х, яке належить області визначення функції, у площині xоyможна побудувати точку М з координатами х₀, f(x₀).Сукупність точок M(x; f(x))називають геометричним зображенням, або графіком функції у = f (x). У загальному випадку це буде якась лінія. Функція вважається заданою графічно, якщо задано її графік.

Табличний спосіб. При експериментальних дослідженнях та спостереженнях залежність між величинами дуже часто подається у вигляді таблиць. Такий спосіб задання функції називається табличним. При табличному способі різним значенням аргументу відповідають певні значення функції. Прикладами табличного задавання функції можуть бути таблиці десяткових логарифмів, таблиці значень тригонометричних функцій, таблиці реєстрації температури хворого протягом дня тощо.

Найчастіше табличним заданням функції користуються в медицині і біології, а саме тоді, коли закон залежності між величинами існує, але невідомий. У цьому разі проводять експеримент, за допомогою якого дістають ряд значень аргументу та відповідних значень функції. Одержані результати записують у вигляді таблиць. Таблиці не будуть точно відображати функціональну залежність, тому що при вимірюванні, хочемо ми того чи ні, матимуть місце похибки, які залежать від класу точності приладів. У цьому полягає недолік табличного задання функції. Крім того, недолік табличного способу полягає ще й в тому, що ми можемо знайти в таблиці не всі, а лише окремі значення функції.

Проте табличний спосіб зручний тим, що при такому задаванні ми без будь-яких обчислень маємо окремі значення функції. А це дуже важливо; іноді навіть функції, задані іншими способами, наприклад аналітично, зображають у вигляді таблиць. Такі таблиці широко використовуються на практиці в медицині.

Крім того, за допомогою таблиць, методом лінійної інтреполяції можна, хоч і наближено, знайти ті значення функції, яких немає і в таблиці І, нарешті, при табличному задаванні легко будувати графіки функції, особливо тоді, коли графік будується по точках.