Приклад: .

Дата добавления: 2014-10-22; просмотров: 759

Знайдемо загальний розв’язок однорідного диференціального рівняння

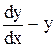= 0.

Відокремимо змінні 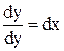. Звідси 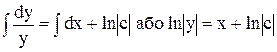. Пропотенціювавши, маємо такий загальний розв’язок диференціального рівняння у=се^х. Для знаходження розв’язку неоднорідного рівняння застосуємо метод варіації довільної сталої. Припустимо, що у формулі у=се^х, с=с(х). Підставимо функцію у диференціальне рівняння. Тоді 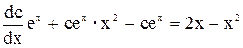. Звідси дістаємо таке диференціальне рівняння: 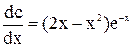. Отже, с= 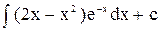. Інтеграл знаходимо частинами. Для цього покладемо u =2x–x² , dv = e^–x, користуючись формулою :

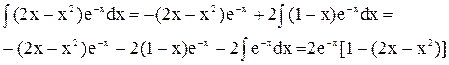
Отже, c = 2e^–x[1–(2x–x²)–2(1–x)] + c. Підставивши знайдено значення с у формулу, знайдемо загальний розв’язок диференціального рівняння

y = ce^x+2[1–(2x–x²) – 2 (1–x)].

Розв’язок деяких медичних задач грунтується на розв’язку диференціальних рівнянь.

Приклад:Швидкість охолодження тіла прямопропорційна різниці температур тіла і навколишнього середовища. До якої температури охолоджується тіло за 30 хвилин, якщо за 10 хвилин воно охолола від 100⁰ до 60⁰С? Температура навколишнього середовища 20⁰С.