Приклади

Дата добавления: 2014-10-22; просмотров: 752

1. Знайти похідну від функції у = х³ + х² + 4х + 1 у точці х₀ = 0.

Знаходимо приріст у у точці х₀ = 0; y = x³ + x² + 4 x, тоді

.

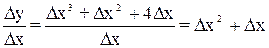
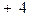Обчислимо границю: = .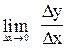

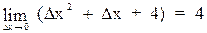Отже, похідна від функції у = х³ + х² + 4х + 1 у точці х₀ = 0 існує і дорівнює 4, тобто 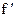(x) = 4.

2. Знайти похідну від функції: 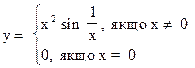у точці х₀ = 0.

Знаходимо приріст у у точці х₀ =0, 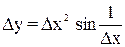, тоді

.

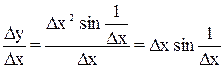Обчислимо границю:

= .

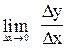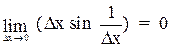Отже, похідна від функції у точці х₀ = 0 існує і дорівнює нулю 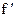(0) = 0.

Функція f(x) в точці x₀ називається диференційованою, якщо в цій точці вона має похідну 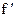(x₀).

Для знаходження похідних елементарних функцій користуються формулами:

y		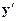y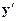
c		cos x	– sin x
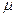
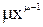
x		tg x	sec2 x
x		ctg x	– cosec2 x
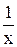
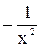
		arcsin x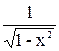
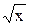
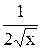
		arccos x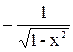
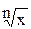
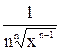
		arctg x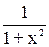
ax	ax lna	arcctg x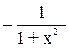
ex	ex	loga x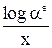
sin x	cos x	ln x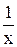

Теореми

Похідна від суми.

Якщо функція f₁(x), f₂(x) в точці х мають похідні, то функція у(х)=f₁(x) 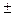f₂(x) також в цій точці має похідну і похідна 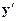(х) дорівнює:

у′=f′ (x) 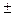f₂′(x).