
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Приклади
Дата добавления: 2014-10-22; просмотров: 807
|
|
Знайти загальний розв’язок диференціального рівняння:
1. y¢¢3 – 2y¢¢– x = 0.
Розв’язок:це рівняння допускає розв’язання відносно х: х = y¢¢3–2y¢¢. Введемо підстановку y¢¢ = t. Тоді x = t3 – 2t. Скористаємося співвідношенням: 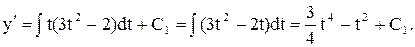
Дістаємо 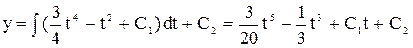 .Отже, загальний розв’язок у параметричній формі має вигляд:
.Отже, загальний розв’язок у параметричній формі має вигляд:
x = t3 – 2t.
у = 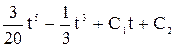 .
.
2. Знайти загальний розв’язок диференціального рівняння 2ху¢¢=y¢.
Розв’язок: застосовуємо підстановку Z = y¢. Тоді рівняння набирає вигляду: 2xZ¢ = Z. Дістали рівняння першого порядку, яке допускає відокремлювання змінних 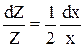 . Звідси знаходимо
. Звідси знаходимо 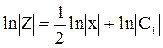 , або Z = C1
, або Z = C1 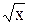 , де С1 – стала інтегрування. Підставимо у рівність значення Z = y¢. Матимемо диференціальне рівняння першого порядку y¢ = C1
, де С1 – стала інтегрування. Підставимо у рівність значення Z = y¢. Матимемо диференціальне рівняння першого порядку y¢ = C1 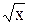 . Загальний розв’язок цього рівняння є:
. Загальний розв’язок цього рівняння є:
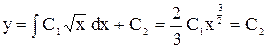 .
.
Дана функція і є зальним розв’язком диференціального рівняння.
3.Знайти рівняння кривої 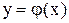 , яка проходить через точку (1; 2), якщо
, яка проходить через точку (1; 2), якщо 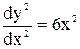 .
.
Розв’язок:інтегруємо диференціальне рівняння 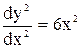 . Якщо
. Якщо 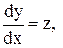 маємо:
маємо:
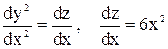 . dz = 6x2dx;
. dz = 6x2dx; 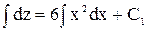 , z = 2x3 + C1, або
, z = 2x3 + C1, або 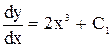 . Інтегруємо це рівняння, знаходимо, що у =
. Інтегруємо це рівняння, знаходимо, що у = 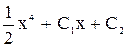 . Підставимо: х = 1, у = 2, одержимо: 3 = 2 + СI, СI = 1.
. Підставимо: х = 1, у = 2, одержимо: 3 = 2 + СI, СI = 1.
2 = 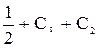 . СI + С2= 1
. СI + С2= 1 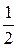 , С2 =
, С2 = 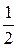 . Рівняння кривої:
. Рівняння кривої: 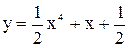 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Диференціальні рівняння вищих порядків. Основні означення і поняття | | | Вимірюванням називається знаходження значення фізичної величини дослідження за допомогою технічних засобів. |