
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Приклади
Дата добавления: 2014-10-22; просмотров: 847
|
|
Знайти невизначені інтеграли, користуючись методом інтегрування за частинами:
1. 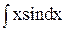 = uv–
= uv– 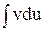 .
.
Введемо позначення u=x; dv=sinxdx. Знаходимо 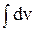 =
= 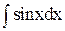 .v = –cosx – сталої при знаходженні v не пишемо. Сталу запишемо при обчисленні інтегралу
.v = –cosx – сталої при знаходженні v не пишемо. Сталу запишемо при обчисленні інтегралу 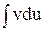 . Оскільки u є відома функція: u = x, то du = u′dx = dx. Отже,
. Оскільки u є відома функція: u = x, то du = u′dx = dx. Отже, 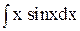 = –xcosx –
= –xcosx – 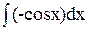 = –xcosx+sinx+c. Якби ми взяли за u=sinx, то ми приклад не розв’язали б.
= –xcosx+sinx+c. Якби ми взяли за u=sinx, то ми приклад не розв’язали б.
2. 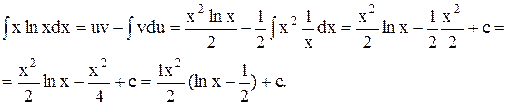
Введемо позначення: u =lnx ; du = 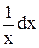 ; dv = xdx, v =
; dv = xdx, v = 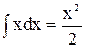 .
.
3. 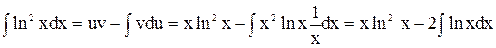 .
.
Введемо позначення: u = ln2x; du = 2lnx 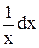 ; dv =dx; dv =
; dv =dx; dv = 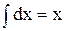 .
.
Невизначений інтеграл 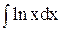 будемо інтегрувати за частинами.
будемо інтегрувати за частинами.
Нехай u = lnx; dv = dx. Тоді du = 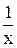 dx, v =
dx, v = 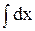 = x.
= x.
Отже, 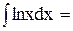 xlnx –
xlnx – 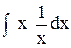 = xlnx – x + с.
= xlnx – x + с.
Остаточно знаходимо 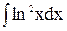 = xln2x –2(xlnx – x) + c.
= xln2x –2(xlnx – x) + c.
4. 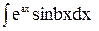 = еах
= еах
Позначимо в цьому інтегралі u = eax , dv = sinbxdx. Звідки du = aeaxdx,
v = 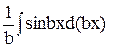 = –
= – 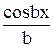 .
.
Тоді 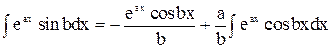 .
.
Інтеграл у правій частині цієї рівності теж обчислюється за частинами. Введемо позначення: u = eax; dv = cos bxdx, звідки du = eaxdx v = 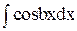 =
= 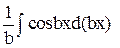 =
= 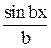 . Скориставшись формулою метода інтегрування за частинами, маємо
. Скориставшись формулою метода інтегрування за частинами, маємо 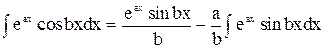 .
.
Підставивши значення цього інтегралу в рівність, дістанемо:
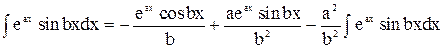 .
.
У правій частині цієї рівності маємо той самий інтеграл, що у лівій. Тому, розв’язуючи цю рівність відносно інтегралу, знаходимо:
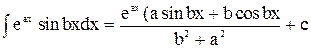 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Приклади | | | Визначений інтеграл |