
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Механічний та геометричний зміст похідної
Дата добавления: 2014-10-22; просмотров: 946
|
|
Нехай функція y = f(x) задана на деякому інтервалі [а;b]. Візьмемо довільну точку х0 Σ[а;b] і надамо х0 довільного приросту  х (число
х (число  х може бути як додатним, так і від’ємним), але такого, щоб точки х0 і х0+
х може бути як додатним, так і від’ємним), але такого, щоб точки х0 і х0+  х належали інтервалу [а;b]. Обчислимо в точці приріст функції
х належали інтервалу [а;b]. Обчислимо в точці приріст функції  у
у
 y = f(x0 +
y = f(x0 +  x) - f(x0).
x) - f(x0).
Означення. Якщо існує границя відношення приросту функції  у до приросту аргументу
у до приросту аргументу  х при умові, що
х при умові, що  х прямує до нуля, тобто
х прямує до нуля, тобто
lim = 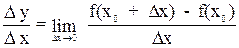 , то границя називається похідною від функції f(x) в точці х = х0 і позначається символом
, то границя називається похідною від функції f(x) в точці х = х0 і позначається символом 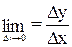 = f′(x0). Для похідної застосовують також і такі позначення:
= f′(x0). Для похідної застосовують також і такі позначення: 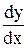 або
або 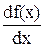 . Поставимо задачу: обчислити швидкість руху точки в момент часу t, якщо точка знаходиться в положенні M (мал. 2).
. Поставимо задачу: обчислити швидкість руху точки в момент часу t, якщо точка знаходиться в положенні M (мал. 2).


 O
O
S
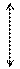
 M
M
 S
S
 M1
M1
Мал. 2
Крім моменту часу t розглянемо момент часу t + 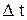 (
( 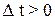 ). Нехай умомент часу t +
). Нехай умомент часу t + 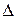 t рухома точка знаходиться в положенні М1. Тоді за час
t рухома точка знаходиться в положенні М1. Тоді за час 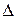 t точка пройде шлях, який позначимо
t точка пройде шлях, який позначимо 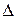 S і називатимемо приростом шляху, цей шлях дорівнює довжині відрізка |ММ1|. За формулою обчислимо приріст
S і називатимемо приростом шляху, цей шлях дорівнює довжині відрізка |ММ1|. За формулою обчислимо приріст 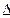 S:
S: 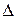 S =
S = 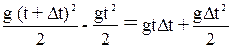 , тоді vc =
, тоді vc = 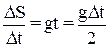 .
.
Отже, на відміну від рівномірного руху, середня швидкість у випадку, що розглядається вже є сталою. Вона при фіксованому моменті часу t залежить від приросту часу 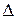 t. При різних значеннях
t. При різних значеннях 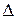 t середня швидкість vc набуває різних значень.
t середня швидкість vc набуває різних значень.
Проте чим менший проміжок часу 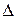 t після моменту часу t, тим, очевидно, середня швидкість буде точніше характеризувати швидкість точки в момент t. Тому природно за швидкість точки в момент часу t прийняти границю vc при
t після моменту часу t, тим, очевидно, середня швидкість буде точніше характеризувати швидкість точки в момент t. Тому природно за швидкість точки в момент часу t прийняти границю vc при 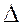 t
t 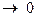 . Швидкістю v точки в момент часу t називається границя середньої швидкості vc на проміжку часу
. Швидкістю v точки в момент часу t називається границя середньої швидкості vc на проміжку часу 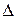 t, коли
t, коли  t прямує до нуля
t прямує до нуля 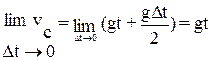 .
.
Отже, швидкість точки в момент t, що вільно падає, дорівнює: v = gt.
Якщо врахувати, що s = f(t) то vc = 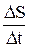 , v =
, v = 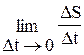 .
.
Знайдемо приріст шляху  S. Для цього часу t надамо приріст
S. Для цього часу t надамо приріст t. Тоді дістанемо вираз для приросту шляху
t. Тоді дістанемо вираз для приросту шляху  S = f(t +
S = f(t +  t) – f (t).
t) – f (t).
Підставивши v = 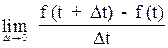 .
.
Зазначимо, що дана формула дає змогу знайти швидкість у момент часу t тільки тоді, коли існує границя цього відношення. Якщо границя цього відношення при якомусь певному значенні t не існує, то кажуть, що рухома точка в цей момент часу швидкості не має.
Розглянемо випадок коли довільна крива L буде задана в декартовій системі координат рівнянням y = f(x), де f(x) – неперервна функція на деякому проміжку [а; b]. Нехай графік цієї функції має вигляд зображений на мал. 3.
L буде задана в декартовій системі координат рівнянням y = f(x), де f(x) – неперервна функція на деякому проміжку [а; b]. Нехай графік цієї функції має вигляд зображений на мал. 3.
|
|
|
|
|
|
|
|
|
|





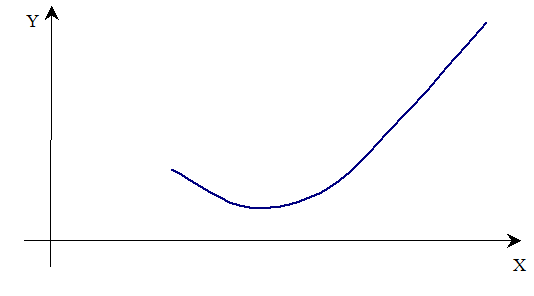
Мал. 3
Візьмемо на кривій точку М0 з координатами (х0, y0) і точку М1 з координатами x0 +  x, y0 +
x, y0 +  y (де
y (де 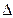 x і
x і  y відповідно прирости х і у, вони можуть бути і від’ємними числами). Через точку М0 і М1 проведемо січну М0М1 і продовжимо її до перетину з віссю Oх. Кут, який утворює січна М0М1 з додатним напрямом осі Охпозначимо через β. Тоді tgβ =
y відповідно прирости х і у, вони можуть бути і від’ємними числами). Через точку М0 і М1 проведемо січну М0М1 і продовжимо її до перетину з віссю Oх. Кут, який утворює січна М0М1 з додатним напрямом осі Охпозначимо через β. Тоді tgβ = 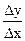 .
.
Якщо точка М1 прямує вздовж кривої L до злиття з точкою М0, то координати точки М1(x0 +  x; y0 +
x; y0 +  y) наближаються як завгодно близько відповідно до координат точки М0 (х0; у0), тобто
y) наближаються як завгодно близько відповідно до координат точки М0 (х0; у0), тобто 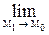 = (x0 +
= (x0 + 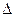 x) = x0,
x) = x0,
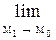 ( y0 +
( y0 +  y) = у0.
y) = у0.
Із співвідношень випливає, що 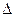 х
х 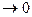 і
і 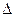 у
у 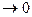 , якщо точка
, якщо точка 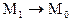 .
.
Нехай тепер 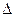 х
х 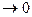 . Тоді й
. Тоді й 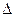 y
y 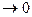 (внаслідок неперервності функції f(x), а отже, точка
(внаслідок неперервності функції f(x), а отже, точка 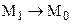 . Таким чином, у даному випадку однієї умови
. Таким чином, у даному випадку однієї умови 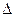 х
х 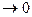 необхідно і достатньо, щоб
необхідно і достатньо, щоб 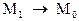 .
.
Припустимо, що розглянута крива в точці М0 має дотичну M0T і утворює з напрямком осі Ох кут α. Тоді кутовий коефіцієнт дотичної M0Tдорівнює tgα. Якщо 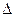 х
х 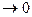 , то кут β прямує до α. Отже, внаслідок неперервності тангенса tg
, то кут β прямує до α. Отже, внаслідок неперервності тангенса tg 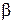
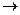 tg
tg 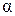 , проте tg
, проте tg 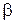 =
= 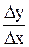 . Тому ми приходимо до такого співвідношення tg
. Тому ми приходимо до такого співвідношення tg 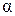 =
= 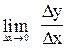 .
.
З даних міркувань випливає такий критерій існування дотичної до кривої. Для того щоб крива у = f(x), де f(x) – неперервна на проміжку [а,b] функція мала в точці М0 дотичну, необхідно і достатньо, щоб існувала границя 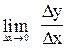 .
.
Приклад: Довести, що дотичною до параболи у = х2 в точці М0(0,0) є вісь абсцес.
Визначимо спочатку кутовий коефіцієнт дотичної, користуючись співвідношенням 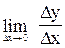 = k . Для цього знаходимо приріст функції f(x)=x2 у точці х0=0. Нагадаємо, що приріст визначається формулою:
= k . Для цього знаходимо приріст функції f(x)=x2 у точці х0=0. Нагадаємо, що приріст визначається формулою:
 y = f(x0 +
y = f(x0 +  x) – f(x0), де
x) – f(x0), де  х = х–х0 – приріст аргументу.
х = х–х0 – приріст аргументу.
У даному випадку  у =
у =  х2, тоді
х2, тоді 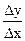 =
=  х і
х і 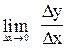 =
= 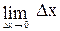 =0. Отже, кутовий коефіцієнт kдотичної до параболи у=х2 в точці М0(0;0) існує і дорівнює нулю, тобто k=0. Підставляючи значення х0=0, у0=0, k=0 дістанемо рівняння дотичної у=0, а це рівняння є рівнянням осі абсцис.
=0. Отже, кутовий коефіцієнт kдотичної до параболи у=х2 в точці М0(0;0) існує і дорівнює нулю, тобто k=0. Підставляючи значення х0=0, у0=0, k=0 дістанемо рівняння дотичної у=0, а це рівняння є рівнянням осі абсцис.
Геометричний зміст похідної випливає із задачі про дотичну. Кутовий коефіцієнт tg 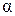 дотичної x, проведений до кривої в точці з координатами x0, у0 = f(x0) дорівнює похідній
дотичної x, проведений до кривої в точці з координатами x0, у0 = f(x0) дорівнює похідній 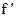 (x0).
(x0).
| <== предыдущая лекция | | | следующая лекция ==> |
| Класифікація функцій | | | Приклади |