Розв’язування

Дата добавления: 2014-10-22; просмотров: 772

Досліджуємо функцію за наведеною схемою.

1. Функція є многочлен, область існування якого є вся множина дійсних чисел, тобто інтервал ] [.

2. Знаходимо точки перетину графіка з координатними осями. При перетинні з віссю 0х (у=0) маємо рівняння 2х⁴-х²+1 = 0. Це рівняння дійсних коренів не має, тобто крива осі 0х не перетинає. Для знаходження точок перетину графіка з віссю 0у покладемо х=0. Маємо у=1. Отже, в точці М₁(0,1) графік функції перетинає вісь 0у.

3. Функція не періодична, але парна. У подальшому досліджуватимемо функцію тільки при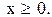

4. Многочлен є функція, неперервна по всій числовій осі. Точок розриву не має.

5. Досліджуємо функцію на кінцях інтервалів. У точці х = 0, маємо у = 1. Знаходимо .

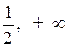6. Для знаходження інтервалів монотонності треба розв’язати нерівності у′ >0, у′<0. У точках, де у′>0, функція зростає, а де у′<0, – спадає. Обчислимо у ′ . у′ = 8х³-2х = 2х(4х²-1)>0, х(4х²–1)>0. Оскільки х>0, то 4х²-1>0, звідси х²> , або х> . Отже, в інтервалі ] [функція зростає, тоді в інтервалі – спадає.

7. Досліджуємо функцію на екстремум. Для цього прирівнюємо першу похідну до нуля х(4х²-1) = 0. Дістанемо такі стаціонарні точки: х₁=0; х₂= (від’ємних значень х не розглядаємо). Точок, в яких у′ не існує, не має. Знайдемо у′′– у′′ = 24x²-2 = 2(12x²-1). Тоді f′′(0) = -2<0, f′′ ( 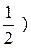= 4>0. Отже, х=0 є точка максимуму, а х₂= – точка мінімуму, причому y_max = f(0)=1. y_min=f( ) = . Таким чином, точки М₁(0;1), М₂( 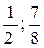) є екстремальні точки.

8. Знаходимо інтервали угнутості та опуклості графіка. Розв’язуємо нерівність y′′>0. 2(12x²-1)>0, 12x²-1>0, x²> , x> . Отже, в інтервалі ] ; + [ крива угнута, а в інтервалі ]0; [ – опукла.

9. Знаходимо точки перетину. Для цього другу похідну прирівнюємо до нуля 2(12х²-1) = 0. Беремо додатковий корінь х₂ = . При переході х через точку х₃, як це випливає з попереднього пункту, y′′змінює знак з “–“ на “+”. Отже, х₃ є абсцисою точки перетину. Знайдемо f(x₃)= 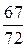. Точка М₃( ) є точкою перетину кривої.

10. Знаходимо асимптоти. Вертикальних асимптот крива не має, бо f(x) не має точок розриву. З’ясуємо, чи є похилі асимптоти. Знаходимо границю . Застосуємо правило Лопіталя:

= .

Отже, крива не має і похилих асимптот (мал.4).