Загальна схема дослідження функції та побудова графіка

Дата добавления: 2014-10-22; просмотров: 1760

Нехай на відрізку [a, b] задана неперервна функція y= f(x). Графіком цієї функції є деяка лінія. Виникає запитання: як побудувати цей графік?

Для побудови графіка функції, треба провести дослідження, до якого входить:

1. Знаходження області існування функції. Це дає змогу визначити ті точки осі абсцис, над якими пройде графік функції, а над якими ні.

2. Знаходження точок перетину графіка з координатними осями. Для цього треба розв’язати дві системи рівнянь:

; .

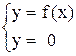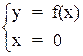Перша система дає точки перетину з віссю 0х, а друга з віссю 0у.

3. Дослідити функцію на періодичність, парність і непарність.

Розв’язування цього питання полегшить побудову графіка в тому розумінні, що побудову доведеться виконувати не в усій області існування функції, а тільки в її частині. Так, якщо f(x) періодична функція з періодом T>0, то графік досить побудувати на відрізку числової осі, довжина якою дорівнює T, а потім цю частину графіка повторити на кожному відрізку довжини T. Якщо функція парна, то графік функції симетричний відносно осі 0у, якщо непарна – то відносно початку координат. Тому достатньо побудувати графік тільки при x>0, а потім симетрично відобразити його і на від’ємні x.

4. Знайти точки розриву функції та дослідити їх характер. Знання характеру точок розриву допоможе встановити вигляд графіка функції поблизу цих точок.

5. Знайти значення функції на кінцях відрізків, де визначена функція. Якщо область існування функції є інтервал (півінтервал) або кілька інтервалів (півінтервалів), то треба знайти граничне значення функції, коли хнаближається до одного з кінців розглядуваних проміжків.

6. Знайти інтервали монотонності функції. Тоді ми знайдемо, де графік піднімається догори, а де опускається донизу.

7. Знайти екстремальні точки і побудувати їх на площині.

8. Знайти інтервали угнутості та опуклості кривої, яка є графіком функції.

9. Знайти точки перетину і побудувати їх на площині.

10. Знайти асимптоти графіка функції.

11. На основі проведеного дослідження побудувати графік функції.

Приклад. Дослідити функцію і побудувати графік: у = 2х⁴-х²+1.