Невизначений інтеграл

Дата добавления: 2014-10-22; просмотров: 697

Основна задача диференціального числення полягає в тому, щоб від заданої функції f(x) знайти її похідну f′(x). Проте на практиці доводиться частіше розв’язувати обернені задачі, коли відома похідна, а потрібно знайти функцію.

Отже, з чисто математичної точки зору ми дістаємо таку задачу. На деякому проміжку (а;b) задано функцію f(x). Треба знайти таку функцію F(x), щоб похідна F′(x) в кожній внутрішній точці проміжку (а;b) дорівнювала б f(x); тобто F′(x) = f(x).

Функція F(x) на проміжку (а; b) називається первісною для функції f(x), якщо F(x) на проміжку(а; b) є неперервною, а в кожній внутрішній точці проміжку (а;b) F(x) є диференційованою і F′ (x) = f(x). Інакше кажучи, якщо F(x) – первісна функція для f(x), то множина всіх первісних функцій для функції f(x) записується рівність F′(x) = f(x)+с, в якій с – довільне стале число. Множина всіх первісних функцій для функції f(x) називається невизначеним інтегралом і позначається 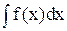. При цьому F(x) називається підінтегральною функцією, а f(x)dx – підінтегральним виразом. Отже, якщо F(x) є первісною для f(x), то .

Знаходження невизначеного інтегралу для функції f(x) називається інтегруванням даної функції.

Розділ математичного аналізу, в якому вивчаються способи інтегрування функцій, називається інтегральним численням.