Властивості визначеного інтегралу

Дата добавления: 2014-10-22; просмотров: 818

Визначений інтеграл має ряд властивостей.

1. = – , якщо у визначеному інтегралі поміняти місцями межі, то при цьому знак інтегралу змінюється на проміжний.

2. – визначений інтеграл з однаковими межами дорівнює нулю.

3. = – сталий множник можна винести за знак визначеного інтегралу.

4. 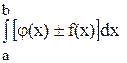= – визначення інтегралу від суми (різниці) функцій дорівнює сумі (різниці) визначених інтегралів від цих функцій.

5. Якщо для функції f(x) існують інтеграли ; ; , то має місце рівність: = + .

Для знаходження визначеного інтегралу користуються формулою Ньютона-Лейбніца = F(b) – F(a), де F(x) – первісна функція f(x), тобто F′(x) = f (x).

Таким чином, щоб знайти визначений інтеграл, необхідно відшукати первісну функцію, підставити в цю первісну – значення верхньої межі, а потім нижньої межі і одержати різницю. У загальному вигляді можна записати = (x F) = F(b)–F(a)