Приклади

Дата добавления: 2014-10-22; просмотров: 681

Розв’язати диференціальні рівняння:

1. у¢= .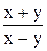

Розв’язання.Права частина заданого рівняння є однорідна функція нульового виміру f(tx, ty ) = 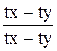= 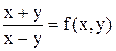. Диференціальне рівняння є однорідним. Застосуємо підстановку y=ux. Маємо 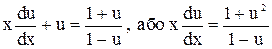. Легко побачити, що умова 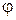(u) – u 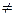0 виконується для всіх u 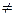1. Проте точки, u = 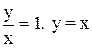не входять в область визначення диференціального рівняння. Отже, відокремлюючи змінні в рівнянні, дістаємо таке диференціальне рівняння: 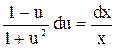. Інтегруючи це рівняння, маємо 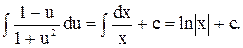Знайдемо інтеграл:

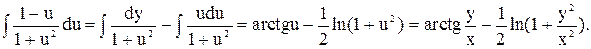Дістанемо такий загальний інтеграл диференціального рівняння:

arctg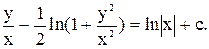

2. .

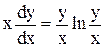Розв’язання. Запишемо це рівняння у вигляді 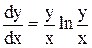. Це однорідне диференціальне рівняння. Зробивши підстановку y=ux, маємо 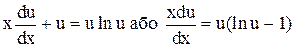. Відокремлюючи змінні, дістаємо .

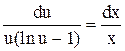Після інтегрування 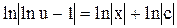. Звідси знаходимо загальний розв’язок: у = хе^ех+1. Відокремлюючи змінні, ми припустили, що u(lnu-1) 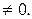Нехай u(lnu-1) = 0, тоді u = 0, u = e. Кореню u = 0 відповідає значення у = 0. Це значення, як видно з рівняння, не належить області визначення заданого рівняння. Кореню u = e, відповідає розв’язок у=ех. Проте цей розв’язок міститься у загальному розв’язку у = хе^ех+1. Його можна дістати із загального розв’язку при с=0. Отже, всі розв’язки диференціального рівняння виражаються формулою у = хе^ех+1.