
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Приклади
Дата добавления: 2014-10-22; просмотров: 874
|
|
Знайти невизначений інтеграл функцій:
1. f(x) = 1 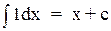
2. f(x) = ex 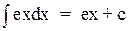
3. f(x) = sinx 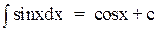
4. f(x) = 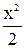
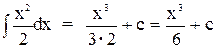
5. f(x) = 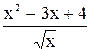
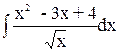 , припустивши, що х
, припустивши, що х 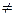 0, підінтегральну функцію можна записати так:
0, підінтегральну функцію можна записати так: 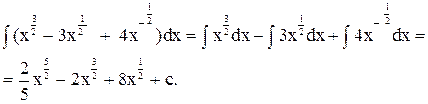
Властивості невизначеного інтегралу
1. Послідовне виконання операції диференціювання та інтегрування в будь-якому порядку з точністю до довільної сталої приводить до початкової функції d( 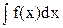 )= f(x)dx
)= f(x)dx  = F(x)+c. Розглянуту властивість можна сформулювати ще так: операції диференціювання та інтегрування з точністю до сталої є взаємно обернені.
= F(x)+c. Розглянуту властивість можна сформулювати ще так: операції диференціювання та інтегрування з точністю до сталої є взаємно обернені.
2. Якщо число а 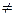 0, то
0, то 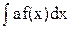 =a
=a 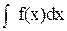 . Дана властивість формулюється так: сталий множник можна виносити за знак невизначеного інтегралу.
. Дана властивість формулюється так: сталий множник можна виносити за знак невизначеного інтегралу.
3. Невизначений інтеграл від суми (різниці) функції дорівнює сумі (різниці) невизначених інтегралів від кожної функції:
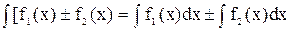 .
.
Основна таблиця інтегралів
| 1. | 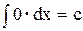
|
| 2. | 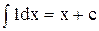
|
| 3. | 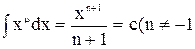
|
| 4. | 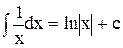
|
| 5. | 
|
| 6. | 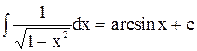
|
| 7. |  ; ; 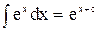
|
| 8. | 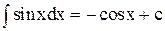
|
| 9. | 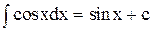
|
| 10. | 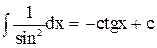
|
| 11. | 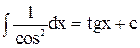
|
| 12. | 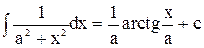
|
| 13. | 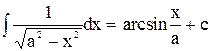
|
| 14. | 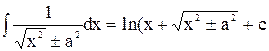
|
| 15. | 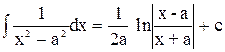
|
| 16. | 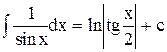
|
| 17. | 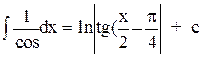
|
| 18. | 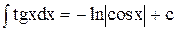
|
| 19. | 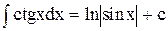
|
| <== предыдущая лекция | | | следующая лекция ==> |
| Невизначений інтеграл | | | Приклади |