Однорідні диференціальні рівняння

Дата добавления: 2014-10-22; просмотров: 1783

Диференціальне рівняння =f(x, y) називають однорідним, якщо функція f(x, y) задовольняє умову f(x, y) = f(tx, ty), де t – будь-яке число, відмінне від нуля. Функція f(x, y), що задовольняє умову, називається однорідною функцією нульового виміру. Тому диференційне рівняння називають однорідним, якщо права частина його є однорідна функція нульового виміру.

Розглядають також функції виміру n, це функції, для яких справджується умова f(tx, ty) = tⁿ f(x, y). При n=0 маємо функцію нульового виміру. Однорідні диференціальні рівняння зводяться до диференціальних рівнянь з відокремлюваними змінними підстановкою y = u(x), де u – невідома функція х, u = u(х). Припустимо, що функція u = u(х) є розв’язком диференціального рівняння = f(x, y). Тоді тотожно виконується рівність x + u =f(x, ux). Проте за умовою, функцію f(x, ux) можна записати так: f(x, ux) = f(tx, tux). Нехай t = 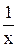(x 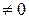). Маємо f(x, ux) = f(1, u), тобто f(1, u) є функція від однієї змінної u f(1, u) = . Диференціальне рівняння набирає вигляду: x , або в диференціальній формі:

xdu = [ 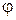(u) – u]dx.

Диференціальне рівняння допускає відокремлювання змінних. Справді, якщо 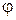(u)–u 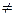0, то рівняння можна записати так: 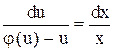, звідси . Підставивши сюди значення u = , дістанемо загальний інтеграл диференціального рівняння. Загальний інтеграл ми знайшли при виконанні умови 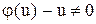. Нехай дана умова не виконується. Тоді матимемо два такі випадки:

1. 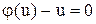, або . У даному випадку диференціальне рівняння набирає вигляду . Загальним розв’язком цього рівняння є сім’я півпрямих у = Сх(х 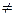0), до яких треба приєднати півпрямі х = (у 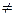0).

2. Умова 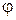(u) – u 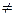0 порушується при окремих значеннях х, наприклад, при u= u₀. Тоді, крім загального інтеграла, диференціальне рівняння має ще розв’язок u = u₀ або у = u₀х, тобто інтегральною кривою є пряма, що проходить через початок координат.