Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Задача про роботу змінної сили
Дата добавления: 2014-10-22; просмотров: 2461
|
|
Якщо на точку М, яка рухається прямолінійна (мал.6), діє стала сила F і її напрям збігається з напрямом руху точки, то робота А, виконана цією силою, дорівнює: A = FS, деS – шлях, пройдений точкою М. Проте здебільшою величина сили не є сталою. Вона неперервна від точки до точки, і користуватися попередньою формулою для обчислення роботи не можна.
A M F(x) Mk Mk+1 B
 |
a x xk Ck xk+1 b x
Мал. 6
Отже, нехай величина сили F є функцією від x. F = F(x) і нехай під дією цієї сили точка М перемістилась з точки A до точки B, пройшовши відстань b–a. Розіб’ємо відрізок[a; b] на n довільних частин точками a = x0 < x1 < x2 < ...< xk < xk+1 < ... < xn-1 < xn = b. Розглянемо відрізок [xk; xk+1] (k = 0,1, ... , n–1). Припустимо, що цей відрізок настільки малий, що F(x) на ньому мало змінюється. Тоді можна вважати, що величина сили дорівнює значенню F(x) в деякій довільно вибраній точці сk, а саме, F = F(ck). Отже, робота, виконана сталою силою F(ck) при переміщенні точки М вздовж прямої з положенняМk в положення Mk+1 , наближено дорівнює:
A F(ck) xk x k = x k+1 – x k. k = 0,1,2, ..., n–1.
Тоді вся робота, виконана силою F при переміщенні точки вздовж прямої з положення Aв положення B, наближено дорівнює:
A = 
.
Зрозуміло, що чим менші будуть довжини частинних відрізків (число 
xk), тим сума, яка стоїть у правій частині попередньої рівності, буде точніше визначення роботи, як ми її інтуїтивно уявляємо. Тому природно за роботуА прийняти A =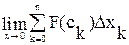 
, 
, 
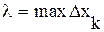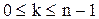, якщо дана границя існує. Тим самим ми дали означення роботи змінної сили F, яку вона виконує при переміщенні точкиM вздовж прямої від точки A до точки B. Обидві задачі звелись до знаходження границь сили. Суму називають інтегральною сумою функції.
Границю інтегральної суми називають визначеним інтегралом функції f(x) на певному відрізку [a; b] і позначають 
(читається: “інтеграл від а до б еф від ікс де ікс”). Число а називається нижньою межею інтегрування;b – верхньою межею; f(x) називається підінтегральною функцією; f(x)dx – підінтегральним виразом; відрізок [a;b] – проміжком інтегрування.
Отже, згідно з визначенням, визначений інтеграл 
є границя (якщо вона існує) інтегральної суми.
| <== предыдущая лекция | | | следующая лекция ==> |
| Визначений інтеграл | | | Властивості визначеного інтегралу |