Похідна від добутку.

Дата добавления: 2014-10-22; просмотров: 871

Якщо функції f₁(x), f₂(x) в точці х мають похідні, то в цій точці функція

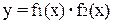також має похідну, яка дорівнює

у′(х) =

Похідна від частки.

Якщо функція f₁(x), f₂(x) в точці х мають похідні і f₂(x) 0, то функція

у = також у точці х має похідну у′ і похідна дорівнює:

y′ = .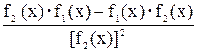

Похідна від складної функції.

Нехай маємо складну функцію у = f(u), u = φ(х) і нехай:

1) зовнішня функція f(u) в точці u₀=φ(х₀) має похідну (по u), ;

2) внутрішня функція u = в точці х₀ має похідну (по х)

Тоді складна функція y = в точці х₀ також має похідну (пох), яка дорівнює добутку з похідної від зовнішньої функції f(u) і похідної від внутрішньої функції (х), тобто або .

Користуючись основною таблицею похідних та теоремами знаходять похідні від функцій, які утворені за допомогою арифметичних операцій та суперпозиції над основними елементарними функціями.