Приклади

Дата добавления: 2014-10-22; просмотров: 712

Розв’язати диференціальні рівняння:

1. .

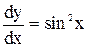Тут права частина є функція, неперервна в усіх точках інтервалу 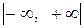. Тому диференціальне рівняння з початковою умовою має єдиний розв’язок:

у = у₀ +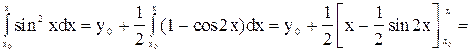

= y₀ + ).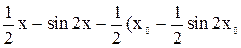

Зокрема, якщо х₀ =0, то у = у + .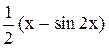

2. 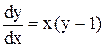, при у 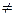1.

Дане рівняння допускає відокремлювання змінних 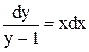. Звідси

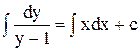. Знайшовши інтервали, маємо ln 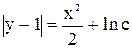. Після потенціювання ln 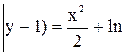, маємо у = 1 + сe 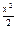. Дістали загальний розв’язок диференціального рівняння.

3. х(у –1)dx + y(x² –1)dy = 0.

Помножимо обидві частини цього рівняння на функцію 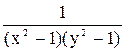. Дістанемо диференціальне рівняння з відокремлюваними змінними .

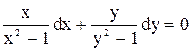Загальний інтеграл, згідно з формулою має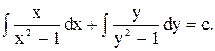

Знайшовши інтеграли, дістанемо ln 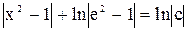. Після потенціювання остаточно маємо такий загальний інтеграл (х²–1)(у²–1) = с. Знайдемо корні рівнянь:

х²–1 = 0, у²–1 = 0.

Маємо х= 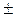1; у= 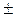1. Отже, прямі х= 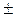1 і у= 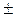1 є інтегральними кривими диференціального рівняння. Проте ці розв’язки знаходяться із загального інтеграла при с=0. Тому вписувати їх не слід. Вони є окремими розв’язками заданого диференціального рівняння.