Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Диференціал функції
Дата добавления: 2014-10-22; просмотров: 833
|
|
Якщо функція y = f(x) в точці x0 диференційована, то її приріст 
у у цій точці можна записати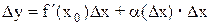 
.
Зазначимо, що доданки в даному рівнянні відіграють різну роль. Так, другий доданок 
при 
є величина вищого порядку малості, ніж х, 
, тоді як перший доданок f′(x0)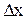 
, якщо і f′(x0) 
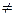0 є величина однакового порядку малості 3 х. Крім того, другий доданок в рівності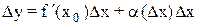 
при і f′(x0) 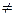0 є величина вищого порядку малості, ніж перша. 
. Отже, перший доданок f′(x0) x в даному рівнянні є головною частиною приросту функції.
Добуток f′(x0) x називається диференціалом функції в точці х0 і позначається символом dy або df(x0).
dy = f′(x0) x, df(x0) = f′(x0) x.
Диференціалом аргументу позначається його приріст, тобто вважають х = dx. Тоді формула для диференціала функції набирає вигляду dy = f′(x0)dx або dy = y′dx. З цієї рівності маємо у′ = 
. Ця рівність читається так: “ігрек штрих дорівнює dy по dx”.
Користуючись співвідношенням dy=y′dx складемо таблицю для диференціалів від елементарних функцій:
| <== предыдущая лекция | | | следующая лекция ==> |
| Розв’язування | | | Невизначений інтеграл |