Розрахунок майбутньої вартості грошових потоків. Майбутня вартість ануїтету

Дата добавления: 2014-11-10; просмотров: 1261

Розглянемо наступний приклад: Нехай інвестор отримує протягом певного період у кінці кожного року певні платежі, які не є однаковими. Якщо він буде інвестувати суму кожного платежу на час до закінчення даного періоду, то після його закінчення отримає деяку суму грошей, яку називають майбутньою вартістю потоку платежів.

Майбутню вартість потоку платежів можна знайти за формулою:

,

де С_t – сума платежу за рік t.

Виникають ситуації, коли, отримують або виплачують не одну суму а декілька, причому рівні суми через однакові проміжки часу і за однієї і тієї ж відсоткової ставки. Такий механізм одержав назву ануїтету або ренти.

Приклади ануїтету: однакові суми коштів, що перераховують щомісяця на депозитний рахунок, однакові щомісячні виплати за кредитом, виплати по облігаціях, регулярні внески до Пенсійного фонду і т.д.

Розрізняють два типи рент (ануїтетів):

– безумовні (з фіксованим строком, коли дати першого і останнього платежів чітко визначені);

– умовні (в яких дати виплати залежать від певної події (пенсійні виплати, страхові виплати).

Види рент (ануїтетів) у залежності від порядку виплати:

– звичайні (постнумерандо), якщо виплати здійснюються у кінці кожного періоду. При цьому майбутня вартість ренти визначається за допомогою декурсивного методу розрахунку платежів (або методу постнумерандо):

;

– авансовані (вексельні або пренумерандо), якщо виплати здійснюються на початку кожного періоду. При цьому майбутня вартість ренти визначається за допомогою антисипативного методу розрахунку платежів (або методу пренумерандо):

;

При використанні схеми платежів при якій кількість нарахувань відсотків та виплат на рік буде більшою від одиниці можливими є 2 варіанти:

– строки нарахування та строки виплат збігаються:

;

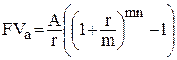– складний відсоток нараховується m разів на рік, а платежі відбуваються тільки в кінці року:

;